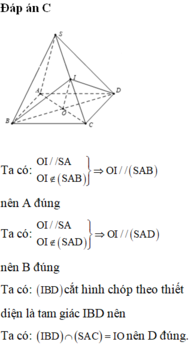
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC . Khẳng định nào sau đây SAI?
![]()
![]()
C. mp (IBD) cắt hình chóp S.ABCD theo thiết diện là một tứ giác
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
+) Ta có:
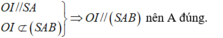
+) Ta có:
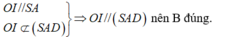
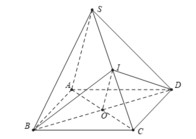
+) Ta có: mp (IBD) cắt hình chóp theo thiết diện là tam giác IBD nên C sai.
+) Ta có: (IBD) ∩ (SAC) = IO nên D đúng.

Đáp án C
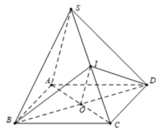
Ta có: O I / / S A O I ∉ S A B ⇒ O I / / S A B nên A đúng
Ta có: O I / / S A O I ∉ S A D ⇒ O I / / S A D nên B đúng
Ta có: (IBD)cắt hình chóp theo thiết diện là tam giác IBD nên
Ta có: I B D ∩ S A C = I O nên D đúng.

Chọn B.
Phương pháp: Xét tính đúng sai của từng mệnh đề.
Cách giải: B sai vì mặt phẳng (IBD) cắt hình chóp S.ABCD theo thiết diện là ∆ I B D

Đáp án C
Phương pháp: Suy luận từng đáp án.
Cách giải:
A đúng.
Ta có IO // SA => IO // (SAB) và IO // (SAD) => B, D đúng.
Mặt phẳng (IBD) cắt hình chóp S.ABCD theo thiết diện chính là tam giác IBD. C sai
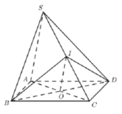

Đáp án B
Gọi P = M N ∩ A C ; I = P K ∩ S O
Do M N / / B D nên giao tuyến của (MNK) với (SBD) song song với MN. Qua I dựng đường thẳng song song với MN cắt SD, SB lần lượt tại E và F khi đó thiết diện là ngũ giác K E M N F