Giải phương trình bằng đồ thị : Cho phương trình 2 x 2 + x – 3 = 0.
Tìm hoành độ của mỗi giao điểm của hai đồ thị. Hãy giải thích vì sao các hoành độ này đều là nghiệm của phương trình đã cho.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) x 2 – x – 2 = 0
Có a = 1; b = -1; c = -2 ⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm x = -1 và x = -c/a = 2.
Vậy tập nghiệm của phương trình là S = {-1; 2}
b) + Đường thẳng y = x + 2 cắt trục Ox tại (-2; 0) và cắt Oy tại (0; 2).
+ Parabol y = x 2 đi qua các điểm (-2; 4); (-1; 1); (0; 0); (1; 1); (2; 4).
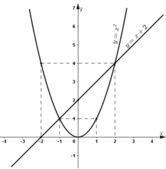
c) Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
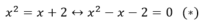
Phương trình (*) chính là phương trình đã giải ở ý (a) Do đó hai nghiệm ở câu (a) chính là hoành độ giao điểm của hai đồ thị

Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
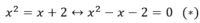
Phương trình (*) chính là phương trình đã giải ở ý (a) Do đó hai nghiệm ở câu (a) chính là hoành độ giao điểm của hai đồ thị

Hướng dẫn làm bài:
a) Giải phương trình: x2 – x – 2 = 0
∆ = (-1)2 – 4.1.(-2) = 1 + 8 > 0
√∆ = √9 = 3
⇒ x1 = -1; x2 = 2
b) Vẽ đồ thị hàm số
- Hàm số y = x2
+ Bảng giá trị:
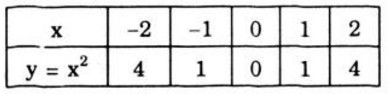
- Hàm số y = x + 2
+ Cho x = 0 ⇒ y = 2 được điểm A(0,2)
+ Cho x = -2 ⇒ y = 0 được điểm B(-2;0)
Đồ thị hàm số:

c) Ta có phương trình hoành độ giao điểm của hai đồ thị là:
x2=x+2⇔x2−x−2=0⇔{x1=−1x2=2x2=x+2⇔x2−x−2=0⇔{x1=−1x2=2
Điều này chứng tỏ rằng đồ thị đường thẳng cắt đồ thị parapol tại hai điểm có hoành độ lần lượt là x = -1; x= 2. Hai giá trị này cũng chính là nghiệm của phương trình x2 - x - 2 = 0 ở câu a).

Đáp án là A.
y ' = x 2 + 2 x ⇒ y ' ' = 2 x + 2 = 0 ⇔ x = − 1 ⇒ y ' − 1 = − 1
Phương trình tiếp tuyến của (C) tại − 1 ; − 4 3 là:
y = − 1 x + 1 − 4 3 = − x − 7 3 .
Ta có: I(-1,5; 4,5), J(1; 2)
*x = -1,5 là nghiệm của phương trình 2 x 2 + x – 3 = 0 vì:
2 - 1 , 5 2 + (-1,5) – 3 = 4,5 – 4,5 = 0
*x = 1 là nghiệm của phương trình 2 x 2 + x – 3 = 0 vì:
2. 1 2 + 1 – 3 = 3 – 3 = 0