Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Tính ∠(BIC) biết rằng: ∠B = 80o,∠C = 40o
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


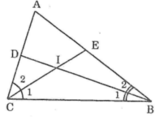
Ta có:
+ Trong ΔBIC có ∠BIC = 180o - (∠B1 + ∠C1) (1)
+ BI, CI là phân giác của ∠ABC và ∠BCA nên:
∠B1 = 1/2. ∠ABC; ∠C1 = 1/2. ∠ACB
⇒ ∠B1 + ∠C1 = 1/2. (∠ABC + ∠ACB) (2)
⇒ ∠ABC + ∠ACB = 180 - ∠A (3).
Từ (1), (2) và (3) suy ra ∠BIC = 180o - 1/2.(180 - ∠A) = 90o + 1/2.∠A
+) Nếu ∠A = 80o ⇒ ∠BIC = 90º + 1/2.80o = 130o.
+) Nếu ∠A = mo ⇒ ∠BIC = 90o + 1/2.mo.

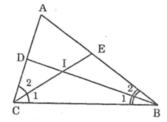
Ta có:
+ Trong ΔBIC có ∠BIC = 180º - (∠B1 + ∠C1) (1)
+ BI, CI là phân giác của ∠ABC và ∠BCA nên:
∠B1 = 1/2. ∠BAC; ∠C1 = 1/2. ∠ACB
⇒ ∠B1 + ∠C1 = 1/2. (∠BAC + ∠BCA) (2)
+ Trong ΔABC có: ∠BAC + ∠BCA = 180 - ∠A =140º (3).
Từ (1), (2) và (3) suy ra ∠BIC = 180º - 1/2.140º = 110º
Chọn đáp án C

Trong tam giác ABC có góc BAC + ABC + ACB = 180 độ
\(\Rightarrow\) góc ABC + góc ACB = 180 độ - góc BAC = 180 độ - 60 độ = 120 (độ)
Ta có góc IBC + góc ICB = góc ABC/2 + góc ACB/2 = (góc ABC + góc ACB)/2 = 120 độ/2 = 60 (độ)
Trong tam giác IBC có góc BIC + góc IBC + góc ICB = 180 độ
\(\Rightarrow\) góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ

a. Hình vẽ ( 0.5 điểm )
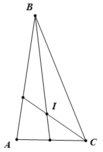
Trong tam giác ABC có:
∠A + ∠(ABC) + ∠(ACB) = 180o
⇒ ∠(ABC) + ∠(ACB) = 180o - 80o = 100o ( 1 điểm )
Mà BI và CI là các tia phân giác nên
∠(ABC) + ∠(ACB) = 2.∠(IBC) +2.∠(ICB) = 2(∠(IBC) + ∠(ICB) ) ( 1 điểm )
Suy ra ∠(IBC) + ∠(ICB) = 50o ( 0.5 điểm )
Mà ∠(IBC) + ∠(ICB) + ∠(BIC) = 180o ⇒ ∠(BIC) = 130o ( 1 điểm )

a. Hình vẽ ( 0.5 điểm )
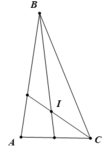
Trong tam giác ABC có:
∠A + ∠(ABC) + ∠(ACB) = 180o
⇒ ∠(ABC) + ∠(ACB) = 180o - 80o = 100o ( 1 điểm )
Mà BI và CI là các tia phân giác nên
∠(ABC) + ∠(ACB) = 2.∠(IBC) +2.∠(ICB) = 2(∠(IBC) + ∠(ICB) ) ( 1 điểm )
Suy ra ∠(IBC) + ∠(ICB) = 50o ( 0.5 điểm )
Mà ∠(IBC) + ∠(ICB) + ∠(BIC) = 180o ⇒ ∠(BIC) = 130o ( 1 điểm )
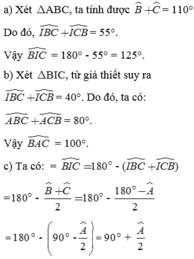
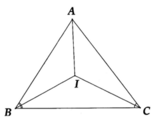
∠B = 80o, ∠C = 40o
Ta có:
∠(B1) = (1/2)∠(ABC) = (1/2).80o = 40o (vì BD là tia phân giác ∠(ABC))
∠(C1) = (1/2)∠(ACB) = (1/2).40o = 20o (vì CE là tia phân giác ∠(ACB))
Trong ΔIBC, ta có: ∠(BIC) + ∠(B1) + ∠(C1) = 180o(tổng 3 góc trong tam giác)
Vậy: ∠(BIC) = 180o - (∠(B1) + ∠(C1)) = 180o - (40o + 20o) = 120o