Chứng minh rằng hàm số:
f x = - 2 x nếu x ≥ 0 sin x 2 nếu x < 0
Không có đạo hàm tại x = 0 nhưng đạt cực đại tại điểm đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 11 2017
Giả sử hàm số f(x) là hàm số chẵn trên đoạn [-a; a], ta có:
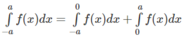
Đổi biến x = - t đối với tích phân
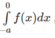
Ta được:
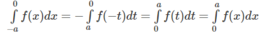
Vậy
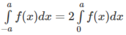
Trường hợp sau chứng minh tương tự. Áp dụng:
Vì 
là hàm số lẻ trên đoạn [-2; 2] nên 
6 tháng 5 2016
Ta có : \(y'=\cos x.e^{\sin x}\Rightarrow y"=-\sin x.e^{\sin x}+\cos^2x.e^{\sin x}\)
\(\Rightarrow y"=-\sin x.y+\cos x.y'\Rightarrow y'\cos x-y.\sin x-y"=0\)
=> Điều phải chứng minh
CM
4 tháng 2 2017
Giả sử hàm số f(x) là hàm số chẵn trên đoạn [-a; a], ta có:
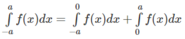
Đổi biến x = - t đối với tích phân
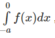
Ta được:
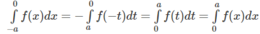
Vậy
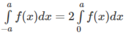
Trường hợp sau chứng minh tương tự. Áp dụng:
Vì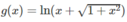 
là hàm số lẻ trên đoạn [-2; 2] nên 
4 tháng 12 2015
Ta có:f(x)=-4x3+x
Khi f(O) thì f(0)=
Cho hàm số: y = f(x)=
khi f(0) thìf(0)= -4*03+0=-12
khi f(-0.5) thì f(-0.5)=-4*(-0.5)+(-0.5)=1.5
chi tiết rồi đó nhớ chọn nha...thanks
=
BS
23 tháng 1 2016
Ta có : y =- f(a)=-(-4.a3+a)=4.a3+-a=a.(4.a2-1) (1)
y = f(-a)=-4.(-a)3+-a=4.a3+-a=a.(4.a2-1) (2)
Từ (1),(2) => f(-a)=-f(a)
Hàm số:
f x = - 2 x nếu x ≥ 0 sin x 2 nếu x < 0
Không có đạo hàm tại x = 0 vì:
Mặt khác, với x < 0 thì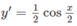
với x > 0 thì y’ = -2 < 0
Bảng biến thiên:
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và y CD = y(0) = 0.