Có bao nhiêu số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3?
A. 5880.
B. 2942.
C. 7440.
D. 3204.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 9 2019
Đáp án là C.
• Sắp xếp bộ ba số 1, 2, 3 sao cho 2 đứng giữa 1,3 có 2 cách.
Số số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3 kể cả trường hợp số 0 đứng đầu là: 2. C 7 4 .5 ! số.
Số số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3, có số 0 đứng đầu là: 2. C 6 3 .4 ! số.
Suy ra số số tự nhiên thỏa yêu cầu bài toán là 2. C 7 4 .5 ! − 2. C 6 3 .4 ! = 7440
CM
29 tháng 6 2018
Đáp án là C.
• Sắp xếp bộ ba số 1, 2, 3 sao cho 2 đứng giữa 1,3 có 2 cách.
Số số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3 kể cả trường hợp số 0 đứng đầu là: 2 . C 7 4 . 5 ! số.
Số số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3, có số 0 đứng đầu là: 2 . C 6 3 . 4 ! số.
Suy ra số số tự nhiên thỏa yêu cầu bài toán là 2 . C 7 4 . 5 ! - 2 . C 6 3 . 4 ! = 7440
CM
29 tháng 6 2019
Đáp án C.
Sắp xếp bộ ba số 1, 2, 3 sao cho 2 đứng giữa 1, 3 có 2 cách.
Số số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3 kể cả trường hợp số 0 đứng đầu là 2. C 7 4 .5 ! số.
Số số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3, có số 0 đứng đầu là 2. C 6 3 .4 ! số.
Suy ra số số tự nhiên thỏa yêu cầu bài toán là 2. C 7 4 .5 ! − 2. C 6 3 .4 ! = 7440 (số)
CM
25 tháng 12 2018
Đáp án C.
Sắp xếp bộ ba số 1, 2, 3 sao cho 2 đứng giữa 1, 3 có 2 cách.
Số số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3 kể cả trường hợp số 0 đứng đầu là 2 . c 7 4 . 5 ! số.
Số số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3, có số 0 đứng đầu là 2 . c 6 3 . 4 ! số.
Suy ra số số tự nhiên thỏa yêu cầu bài toán là 2 . c 7 4 . 5 ! - 2 . c 6 3 . 4 ! = 7440 (số).
8 tháng 4 2023
TH1: Phải chứa bộ 519
Lấy 4 số trong tập A={0;2;3;4;6;7;8} có \(A^4_7\left(cách\right)\)
Cài bộ 519 vào vị trí đầu, cuối hoặc giữa thì có 5 cách
=>Có 5*A47=4200 số
Trong các số nói trên thì có \(4\cdot A^3_6=480\) số có chữ số 0 đứng đầu
=>Có 3720 số
TH2: Có bộ số 915
Cũng có 3720 số thỏa mãn
=>CÓ 3720*2=7440 số
CM
25 tháng 4 2019
Xét hai trường hợp:
Trường hợp 1: Số phải tìm chứa bộ 123.
Lấy 4 chữ số ∈ 0 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 : có A 7 4 cách
Cài bộ 123 vào vị trí đầu, hoặc cuối, hoặc giữa hai chữ số liền nhau trong 4 chữ số vừa lấy: có 5 cách.
Suy ra có 5 A 7 4 = 5 . 840 = 4200 số gồm 7 chữ số khác nhau trong đó chứa bộ 123
Trong các số trên, có 4 A 6 3 = 4 . 120 = 480 số có chữ số 0 đứng đầu.
Suy ra có 5 A 7 4 - 4 A 6 3 = 3720 số phải tìm trong đó có mặt bộ 123
Trường hợp 2: Số phải tìm có mặt bộ 321 (lập luận tương tự)
Có 3720 số gồm 7 chữ số khác nhau, có mặt 321
Tóm lại, có 3720.2 = 7440 số gồm 7 chữ số khác nhau đôi một, trong đó chữ số 2 đứng liền 2 chữ số 1 và 3
Đáp án D
CM
5 tháng 2 2017
Đáp án B
Gọi số cần tìm có dạng a b c d e f .
Số cần tìm có dạng 154 d e f . Khi đó d có 7 cách chọn, e có 6 cách chọn, f có 5 cách chọn.
=> có 210 cách chọn.
Số cần tìm có dạng a 154 e f . Khi đó a có 6 cách chọn, e có 6 cách chọn, f có 5 cách chọn.
=> có 180 cách chọn.
Hai khả năng a b 154 f và a b c 154 cũng có số cách chọn như a 154 e f .
Suy ra có tổng số cách chọn là: (210 + 180.3) = 750.
CM
30 tháng 11 2018
Đáp án B
Gọi số cần tìm có dạng a b c d e f ¯ .
· Số cần tìm có dạng 154 d e f ¯ . Khi đó d có 7 cách chọn, e có 6 cách chọn, f có 5 cách chọn.
có 210 cách chọn.
· Số cần tìm có dạng a 154 e f ¯ . Khi đó a có 6 cách chọn, e có 6 cách chọn, f có 5 cách chọn.
có 180 cách chọn.
Hai khả năng a b 154 f ¯ và a b c 154 ¯ cũng có số cách chọn như a 154 e f ¯ .
Suy ra có tổng số cách chọn là: 210 + 180.3 .2 = 750
Đáp án C.
Sắp xếp bộ ba số 1, 2, 3 sao cho 2 đứng giữa 1, 3 có 2 cách.
Số số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3 kể cả trường hợp số 0 đứng đầu là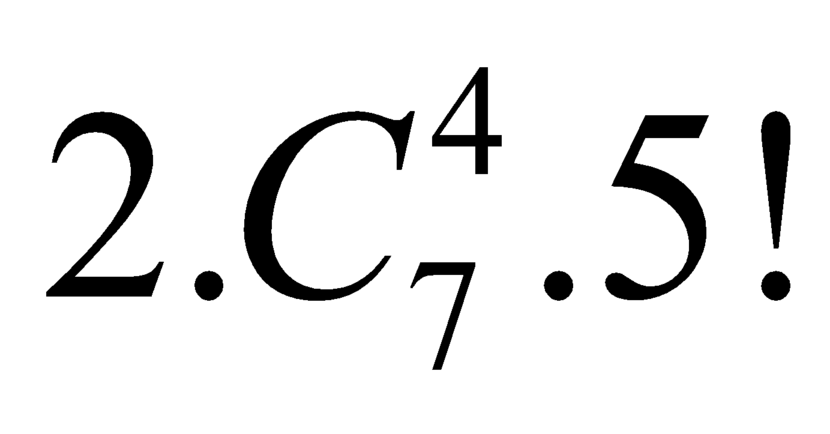
số.
Số số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 2 đứng liền giữa hai chữ số 1 và 3, có số 0 đứng đầu là
số.
Suy ra số số tự nhiên thỏa yêu cầu bài toán là
(số).