Cho hai số phức z 1 , z 2 thỏa mãn điều kiện z 1 = z 2 = 1 và z 1 + z 2 = 3 . Biết rằng , trong đó m, n, p là các số nguyên dương và phân số m p tối giản. Tính S = 15 m + 12 n + 2019 p .
A. 2087
B. 4159
C. 6093
D. 4087
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi M(x;y) biểu diễn cho z, ta có hệ
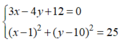
Để ý đường thẳng ![]() tiếp xúc với đường tròn
tiếp xúc với đường tròn ![]() , nên chỉ có một số phức.
, nên chỉ có một số phức.

Đáp án A
Đặt z = x + yi với x,y ∈ ℝ , ta có:
![]()
![]()
![]() = 5x - 5yi
= 5x - 5yi
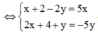
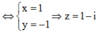
Do đó ![]()
![]()
Vậy w có phần ảo bằng 2 1009

Đáp án D
Phương pháp:
- Biểu diễn số phức và giải bài toán tìm GTLN trên mặt phẳng tọa độ.
Cách giải: Gọi I(1;1), J(-1;-3), A(2;3).
Xét số phức ![]() , có điểm biểu diễn là M(x;y)
, có điểm biểu diễn là M(x;y)
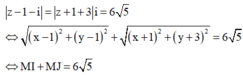
![]() M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
3
5
M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
3
5
Tìm giá trị lớn nhất của ![]() tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
Ta có:
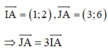
điểm A nằm trên trục lớn của elip.
![]() AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
Gọi S là trung điểm của IJ
![]() S(0;-1)
S(0;-1)
Độ dài đoạn AB=SA+SB
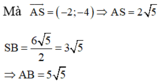
Vậy ![]()
Chọn đáp án D.
nên kết hợp với các đẳng thức ở trên, ta được
Tổng quát bài toán chúng ta có kết quả sau:
trong đó m, n, p là độ dài ba cạnh của một tam giác thì