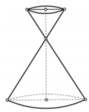
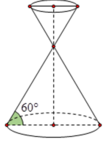
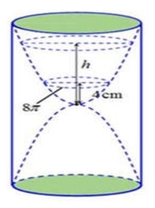
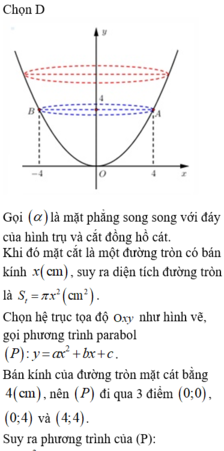
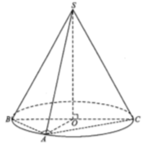
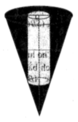
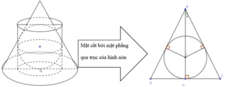
Cho một đồng hồ cát như hình bên dưới (gồm 2 hình nón chung đỉnh ghép lại), trong đó đường sinh bất kỳ của hình nón tạo với đáy một góc 60 ° . Biết rằng chiều cao của đồng hồ là 30cm và tổng thể tích của đồng hồ là 1000 π c m 3 . Hỏi nếu cho đầy lương cát vào phân trên thì chảy hết xuống dưới, khi đó tỷ lệ thể tích lượng cát chiếm chỗ vào thể tích phần phía dưới là bao nhiêu?
A. 1 3 3
B. 1 8
C. 1 64
D. 1 27

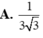
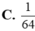

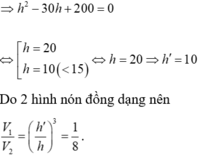

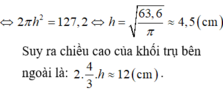
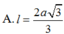
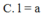

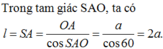
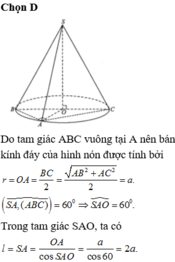
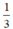 π
m
2
k
π
m
2
k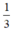 thể tích hình trụ. Do đó, khi chứa đầy cát vào hình nón rồi đổ hết sang hình trụ thì độ cao của cát trong hình trụ sẽ là
thể tích hình trụ. Do đó, khi chứa đầy cát vào hình nón rồi đổ hết sang hình trụ thì độ cao của cát trong hình trụ sẽ là 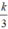
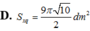


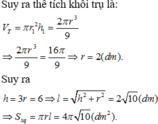



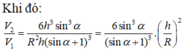
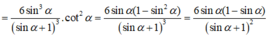
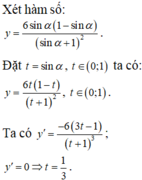
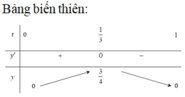
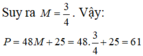
Đáp án B
Gọi r , h , r ' , h ' lần lượt là bán kính và chiều cao của hình nón lớn và nhỏ
Phân tích dữ kiện
+) Chiều cao của đồng hồ là 30 cm ⇔ h + h ' = 30 c m
+) Tổng thể tích của đồng hồ là 1000 π c m 3
⇔ V l + V n = π r 2 h + π r ' 2 h ' 3 = 1000 π ⇔ r 2 h + r ' 2 h ' = 3000
+) Đường sinh bất kỳ của hình nón tạo với đáy một góc 60 ° ⇔ h r = h ' r ' = 3
Ta có hệ:
h + h ' = 3 r + r ' r 2 h + r ' 2 h ' = 3 r 3 + r ' 3 = 3000 ⇔ 3 r + r ' 3 = 9000 3 r 3 + r ' 3 = 3000 ⇔ r + r ' 3 r 3 + r ' 3 = 3
⇔ 2 r ' 2 − 5 r r ' + 2 r 2 = 0 ⇔ r r ' = 1 2
vì 0 < r ' < r
Theo đó tỉ lệ cần tính là:
V n V l = r ' 2 h ' r 2 h = r ' r 3 = 1 8