Với giá trị nào của x thì A = |x − 3| + |x − 5| + |x − 7| đạt giá trị nhỏ nhất?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
2
2 tháng 11 2016
Nhận thấy: |x-7|=|7-x|
Áp dụng BĐT: |a|+|b| \(\ge\) |a+b|
=> |x-3|+|7-x| \(\ge\) |x-3+7-x| = 4
=> |x-3|+|7-x| \(\ge\) 4
Dấu "=" xảy ra khi 3\(\le\)x\(\le\) 7 (1)
Lại có: |x-5| \(\ge\) 5
Dấu "=" xảy ra khi x = 5 (2)
Vậy A đạt giá trị nhỏ nhất là 4 khi x = 5
3 tháng 11 2016
Khi X=5
Give me a tick, pleaseeeeeeeeeeeeeeeeeeeeeee
3 tháng 2 2019
A=|x-3|+|x-5|+|7-x| >= |x-3+7-x|+|x-5|=|4|+|x-5|=4+|x-5|
vì |x-5|>=0 với mọi x
=>A>=4+0=4
dấu "=" xảy ra khi
(x-3)(7-x)>=0 va x-5=0
<=>x>=3 và x<=7 va x=5
suy ra GTNN của A=4 khi x=5
PT
1
22 tháng 10 2015
A=|x-3|+|x-5|+|x-7|=|x-3+7-x|+|x-5|
=|-4|+|x-5|=4+|x-5|
Ta có: |x-5|>=0 với mọi x
|x-5|+4>=4 hay A>=4
Do đó, GTNN của A là 4 khi:
x-5=0
x=0+5
x=5
Vậy GTNN của A là 4 khi x=5
HV
2
B
23 tháng 8 2017
Bài làm
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
LN
0
CN
0
PN
1
21 tháng 8 2015
A=|x-3|+|x-5|+|7-x| >= |x-3+7-x|+|x-5|=|4|+|x-5|=4+|x-5|
vi |x-5|>=0 voi moi x
=>A>=4+0=4
dau "=" xay ra khi va chi khi:
(x-3)(7-x)>=0 va x-5=0
<=>x>=3 va x<=7 va x=5
vay GTNN cua A=4 khi va chi khi x=5
QN
0
Ta có:
|x – 3| + |x – 7| = |x – 3| + |7 – x| ≥ |x – 3 + 7 – x| = |4| = 4.
(áp dụng bài 140: |x| + |y| ≥|x + y|)
* Lại có: |x – 5| ≥ 0.
Vậy A = |x – 3| + |x – 5| + |x – 7| ≥ 4 + 0 = 4.
Dấu ''='' xảy ra khi và chỉ khi: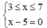
, tức là x = 5.
Vậy với x = 5 thì A đạt giá trị nhỏ nhất là 4.