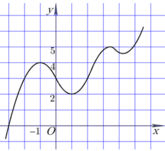
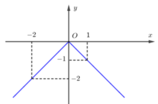
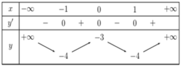
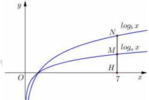
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Tìm số giá trị nguyên của m để phương trình
f
(
x
2
-
2
x
)
=
m
có đúng 4 nghiệm thực phân biệt thuộc đoạn
[
-
3
2
;
7
2
]
.
A. 1
B. 4
C. 2
D. 3



Đáp án đúng : C