Tìm tập xác định của các hàm số
y = - x 5 + 7 x - 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
8 tháng 7 2021
1.Ý C
Hàm số có nghĩa khi \(x^2+14x+45\ne0\Leftrightarrow x\ne\left\{-5;-9\right\}\)
\(\Rightarrow D=R\backslash\left\{-5;-9\right\}\)
2. Ý D
Hàm số có nghĩa khi \(\left\{{}\begin{matrix}x+7\ge0\\x^2+6x-16\ne0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x\ge-7\\x\ne\left\{2;-8\right\}\end{matrix}\right.\)
\(\Rightarrow D=\)\([-7;+ \infty) \)\(\backslash\left\{2\right\}\)
21 tháng 9 2021
ĐK : \(x^2+14x+45\ne0\)
\(\Leftrightarrow\hept{\begin{cases}x\ne-5\\x\ne-9\end{cases}}\)
\(TXĐ:D=R\backslash\left\{-5;-9\right\}\)
Chọn C
PT
1
PT
1
CM
26 tháng 11 2017
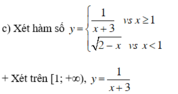
Hàm số xác định khi x + 3 ≠ 0 (luôn thỏa mãn với mọi x ≥ 1).
Vậy hàm số luôn xác định trên [1; +∞).
+ Xét trên (–∞; 1), .
Hàm số xác định khi 2 – x ≥ 0 ⇔ x ≤ 2 (Luôn thỏa mãn với mọi x < 1).
Vậy hàm số luôn xác định trên (–∞; 1).
Kết luận: Hàm số xác định trên R.
CM
3 tháng 11 2019
Đáp án D.
Ta có hàm số y = x − 1 − 7 có lũy thừa với số mũ nguyên âm là –7 nên cơ số x − 1 ≠ 0 ⇔ x ≠ 1
PT
1
MP
0
D = R