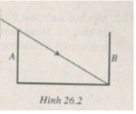
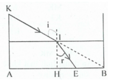
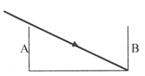
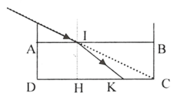
Một cái máng nước sâu 30 cm, rộng 40 cm có hai thành bên thẳng đứng. Đúng lúc máng cạn nước thì có bóng râm của thành A kéo dài tới đúng chân thành B đối diện (Hình 26.2). Người ta đổ nước vào máng đến một độ cao h thì bóng của thành A ngắn bớt đi 7 cm so với trước. Biết chiết suất của nước là n = 4/3. Hãy tính h và vẽ tia sáng giới hạn bóng râm của thành máng khi có nước.


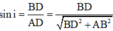
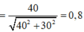
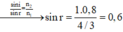



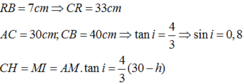
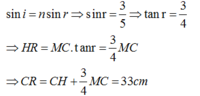
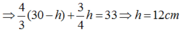


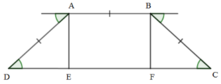

CC’ = 7cm
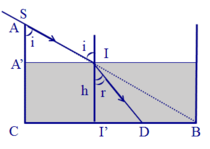
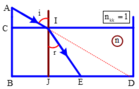
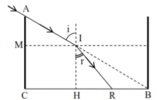
→ HC – HC’ = h(tani – tanr) = 7cm (Hình 26.1G).
Do đó