Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Chọn trục tọa độ Ox có chiều trùng cới chiều chuyển động của người đi xe máy và xe buýt, chiều dương hướng từ người đi xe máy đến xe buýt. Gốc O tại vị trí xuất phát của người đi xe máy. Gốc thời gian là lúc người và xe buýt bắt đầu chuyển động.
Tại thời điểm t:
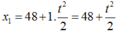
Vị trí của xe buýt :
Vị trí của người đi xe máy:
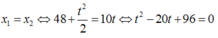
Khi người đi xe máy bắt kị xe buýt thì
Như vật thời gian nhỏ nhất để người đi xe máy bắt kịp xe buýt là 8 s, sau đó người đi xe máy sẽ vượt lên xe buýt. Tại t2 = 12s xe buýt sẽ lại đuổi kịp xe máy. Sau thời điểm này, xe buýt luôn ở trước xe máy.
Lời giải
Sau va chạm 2 vật dính vào nhau và cùng chuyển động với cùng một vận tốc => 2 vật va chạm mềm.
Chọn chiều dương là chiều chuyển động của viên đạn
Gọi v 1 , v 2 , V lần lượt là vận tốc viên đạn, xe lúc trước là xe lúc sau va chạm. Ta có:
m 1 v 1 + m 2 v 2 = m 1 + m 2 V ⇒ V = m 1 v 1 + m 2 v 2 m 1 + m 2 ⇔ 7 , 4 = m 1 .600 − 1 , 5.0 , 5 m 1 + 1 , 5 ⇔ m 1 = 0 , 02 k g = 20 g
Với v 2 = − 0 , 5 m / s vì xe chuyển động ngược chiều so với viên đạn
Đáp án: A
Đáp án C.
Chọn chiều dương của trục Ox cùng hướng chuyển động của người và xe, gốc O tại vị trí ban đầu của người. Gốc thời gian là lúc người và xe bắt đầu chuyển động.
Vị trí của người và xe buýt sau khoảng thời gian t:
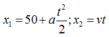
Khi người bắt kịp xe buýt:
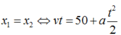
Điều kiện phương trình phải có nghiệm t > 0
Vậy giá trị nhỏ nhất của v để người đó bắt kịp xe buýt là 10 m/s
a,Gia tốc của xe :\(a=\dfrac{20-4}{20}=\dfrac{4}{5}\left(\dfrac{m}{s^2}\right)\)
Quãng đường đi được trong khoảng thời gian 20s
\(s=4\cdot20+\dfrac{1}{2}\cdot\dfrac{4}{5}\cdot20^2=240\left(m\right)\)
b,Tốc độ xe đạt dc sau 12 s tăng tốc
\(v=4+\dfrac{4}{5}\cdot12=13,6\left(\dfrac{m}{s}\right)\)
c, Thời gian để xe đi dc 800 m
\(800=4t+\dfrac{1}{2}\cdot\dfrac{4}{5}\cdot t^2\Rightarrow t=40\left(s\right)\)
Đáp án C