Cho đường thẳng d : x − 2 − 1 = y + 1 − 1 = z + 1 1 và mặt phẳng P : 2 x + y − 2 z = 0. Đường thẳng ∆ nằm trong (P), cắt d và vuông góc với d có phương trình là:
A. x = 1 − t y = − 2 + t z = − t .
B. x = 1 − t y = − 2 z = − t .
C. x = 1 − t y = − 2 z = t .
D. x = 1 + t y = − 2 z = − t .


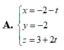
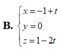
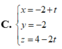
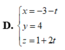
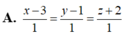
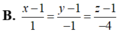
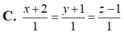
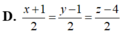
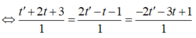
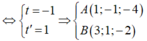






Đáp án B.
Gọi A = d ∩ P ⇒ A − t + 2 ; − t − 1 ; t − 1
⇒ 2 − t + 2 + − t − 1 − 2 t − 1 = 0 ⇔ − 5 t + 5 = 0 ⇔ t = 1 ⇒ A 1 ; − 2 ; 0 .
Ta có:
u d → = − 1 ; − 1 ; 1 u p → = 2 ; 1 ; − 2 ⇒ u d → ; u p → = 1 ; 0 ; 1 ⇒ Δ : x = 1 − t y = − 2 z = − t t ∈ ℤ .