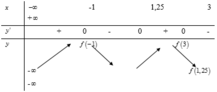
Cho hàm số f x = m x 4 + n x 3 + p x 2 + q x + r ( m , n , p , q , r ∈ R ) . Hàm số y=f'(x) có đồ thị như hình vẽ bên. Tập nghiệm của phương trình f(x)=r có số phần tử là
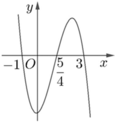
A. 4
B. 3
C. 1
D. 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

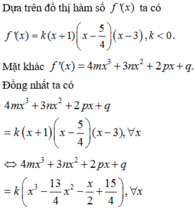
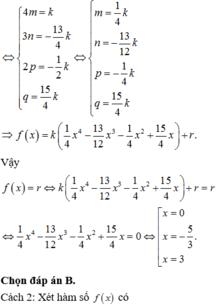
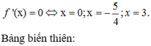


1, BPT đúng với mọi x thuộc R khi vầ chỉ khi:
\(\left\{{}\begin{matrix}a>0\\\Delta\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a>0\\1-4a^2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a>0\\a\le\frac{-1}{2};a\ge\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow a\ge\frac{1}{2}\)
2, điều kiện: \(\Delta< 0\\ \Leftrightarrow\left(m+2\right)^2+8\left(m-4\right)< 0\\ \Leftrightarrow m^2+12m-28< 0\\ \Leftrightarrow-14< m< 2\)
3, điều kiện: \(\Delta'< 0\\ \Leftrightarrow\left(2m-3\right)^2-\left(4m-3\right)< 0\\ \Leftrightarrow m^2-4m+3< 0\\ \Leftrightarrow1< m< 3\)
4, Nếu m=0 => f(x)=-2x-1<0 (loại)
Nếu m≠0 để f(x)<0 với ∀x ϵ R khi và chỉ khi:
\(\left\{{}\begin{matrix}m< 0\\\Delta'< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 0\\1+m< 0\end{matrix}\right.\)
\(\Rightarrow m< -1\)

Đặt \(y=f\left(x\right)\Leftrightarrow x+y^3+2y=1\Leftrightarrow x=-y^3-2y+1\)
\(\Rightarrow dx=\left(-3y^2-2\right)dy\)
\(x=-2\Rightarrow-y^3-2y+1=-2\Rightarrow y=1\)
\(x=1\Rightarrow-y^3-2y+1=1\Rightarrow y=0\)
\(\Rightarrow\int\limits^1_{-2}f\left(x\right)dx=\int\limits^0_1y\left(-3y^2-2\right)dy=\int\limits^1_0\left(3y^3+2y\right)dy=\frac{7}{4}\)

Thay \(x=2\) vào ta được:
\(f\left(2\right)+3f\left(\dfrac{1}{2}\right)=4\Rightarrow f\left(\dfrac{1}{2}\right)=\dfrac{4-f\left(2\right)}{3}\) (1)
Thay \(x=\dfrac{1}{2}\) vào ta được:
\(f\left(\dfrac{1}{2}\right)+3f\left(2\right)=\dfrac{1}{4}\) (2)
Thay (1) vào (2):
\(\dfrac{4-f\left(2\right)}{3}+3f\left(2\right)=\dfrac{1}{4}\Rightarrow\dfrac{8}{3}f\left(2\right)=\dfrac{-13}{12}\)
\(\Rightarrow f\left(2\right)=\dfrac{-13}{32}\)