Xác định tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức sao cho z − i z + i là số thực.
A. Đường tròn phương trình x 2 + y 2 = 1 bỏ đi điểm (0;−1).
B. Trục tung bỏ đi điểm (0;−1).
C. Hyperbol phương trình x 2 − y 2 = − 1 bỏ đi điểm (0;−1).
D. Trục hoành bỏ đi điểm (0;1).

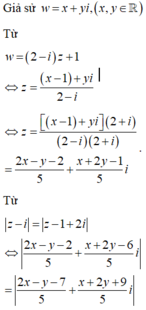
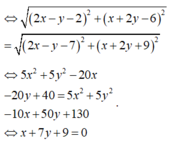


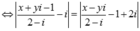


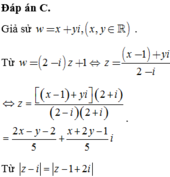
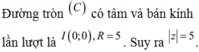
Đáp án B
Gọi z = x + i y ; x , y ∈ ℝ .
z − i z + i = x + i y − 1 x + i y + 1 = x + i y − 1 x − i y + 1 x 2 + y + 1 2 = x 2 + y 2 − 1 + i x y − 1 − x y + 1 x 2 + y + 1 2 = x 2 + y 2 − 1 x 2 + y + 1 2 + i − 2 x x 2 + y + 1 2 .
z − i z + i là số thực ⇔ − 2 x x 2 + y + 1 2 = 0 ⇔ x = 0 x ≠ 0 ; x ≠ − 1 là trục tung bỏ đi điểm (0;−1).