Các đường cao hạ từ A và B của tam giác ABC cắt nhau tại H (góc C khác 90 ° ) và cắt đường tròn ngoại tiếp tam giác ABC lần lượt tại D và E. Chứng minh rằng:
a) CD = CE ; b) ΔBHD cân ; c) CD = CH.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 5 2019
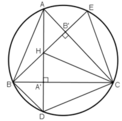
* Cách 1.
Ta có: AD vuông BC tại A' nên A A ' B ^ = 90 o
Vì A A ' B ^ là góc có đỉnh bên trong đường tròn nên:
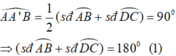
Tương tự, vì BE vuông góc AC tại B' nên ta có:
E B ' C ^ là góc có đỉnh nằm trong đường tròn
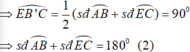
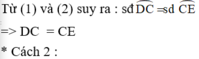
Ta có:
(1)
Và 
(2)
Tà (1) và (2) 
Đây là hai góc nội tiếp chắc hai cung DC và CE nên:
CM
26 tháng 9 2018
Từ tam giác cân BHD suy ra HA'=A'D (BA' là đường trung trực của cạnh HD)
Điểm C nằm trên đường trung trực của HD nên CH=CD.
CM
21 tháng 2 2017
Do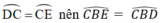 
( hai góc nội tiếp chắn hai cung bằng nhau).
Suy ra: BC là tia phân giác của góc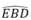 
.
Xét tam giác BHD có BA’ vừa là đường cao vừa là đường phân giác nên tam giác BHD cân tại B.
22 tháng 3 2020
a) Gọi M,N lần lượt là giao điểm của AD với BC và BE với AC
Các \(\hept{\begin{cases}\widehat{ANB}\\\widehat{AMB}\end{cases}}\)là 2 góc có đỉnh nằm bên trong đường tròn nên ta có:
\(\widehat{ANB}=\frac{1}{2}\)(sđ \(\widebat{EC}\)+ sđ \(\widebat{AB}\)) =90o (vì BE_|_ AC)
\(\widehat{AMB}=\frac{1}{2}\)(sđ \(\widebat{DC}\)+ sđ \(\widebat{AB}\))=90o (vì AD _|_ BC)
Vậy ta có: \(sđ\widebat{CE=sđ\widebat{CD}}\)\(\Leftrightarrow CD=CE\left(đpcm\right)\)
Nguồn: loigiaihay.com
16 tháng 2 2021
a) Gọi G là trung điểm của BC
Ta có: ΔDBC vuông tại D(BD\(\perp\)AC tại D)
mà DG là đường trung tuyến ứng với cạnh huyền BC(G là trung điểm của BC)
nên \(DG=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(1)
Ta có: ΔEBC vuông tại E(CE\(\perp\)AB)
mà EG là đường trung tuyến ứng với cạnh huyền BC(G là trung điểm của BC)
nên \(EG=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(2)
Ta có: G là trung điểm của BC(gt)
nên \(BG=CG=\dfrac{BC}{2}\)(3)
Từ (1), (2) và (3) suy ra GB=GC=GE=GD
hay B,C,D,E cùng nằm trên một đường tròn(đpcm)
a) * Cách 1.
b) Do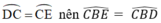
( hai góc nội tiếp chắn hai cung bằng nhau).
Suy ra: BC là tia phân giác của góc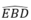
.
Xét tam giác BHD có BA’ vừa là đường cao vừa là đường phân giác nên tam giác BHD cân tại B.