Cho hai đường tròn O 1 ; 5 và O 2 ; 5 cắt nhau tại 2 điểm A,B sao cho AB là 1 đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi 2 đường tròn (ở ngoài đường tròn lớn, phần tô màu như hình vẽ). Quay (D) quanh trục O 1 ; O 2 ta được 1 khối tròn xoay. Tính thể tích khối tròn xoay được tạo thành.
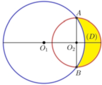
A. V = 36 π .
B. V = 68 π 3 .
C. V = 14 π 3 .
D. V = 40 π 3 .


Đáp án D.
Gắn hệ trục tọa độ Oxy sao cho O 1 ≡ O (gốc tọa độ).
Phương trình đường tròn O 1 ; 5 là x 2 + y 2 = 5 2 ⇒ y = ± 25 − x 2 .
Tam giác O 1 O 2 A vuông tại O 2 , có O 1 O 2 = O 1 A 2 − O 2 A 2 = 5 2 − 3 2 = 4.
Phương trình đường tròn O 2 ; 3 là x − 4 2 + y 2 = 9 ⇒ y = ± 9 − x − 4 2 .
Gọi V 1 là thể tích của khối tròn xoay sinh ra khi quay hình phẳng D 1 được giới hạn bởi các đường y = 9 − x − 4 2 , y = 0 , x = 4 , x = 7 quanh trục tung ⇒ V 1 = π ∫ 4 7 9 − x − 4 2 d x .
Gọi V 2 là thể tích của khối tròn xoay sinh ra khi quay hình phẳng D 2 được giới hạn bởi các đường y = 25 − x 2 , y = 0 , x = 4 , x = 5 quanh trục tung ⇒ V 2 = π ∫ 4 5 25 − x 2 d x .
Khi đó, thể tích cần tính là:
V = V 1 − V 2 = π ∫ 4 7 9 − x − 4 2 d x − π ∫ 4 5 25 − x 2 d x = 40 π 3 .