Hai con lắc lò xo giống nhau gồm lò xo nhẹ và vật nặng có khối lượng 500 g, dao động điều hòa với phương trình lần lượt là x 1 = A cos ( ω t - π 3 ) c m và x 2 = 3 A 4 cos ( ω t + π 6 ) c m trên hai trục tọa độ song song cùng chiều gần nhau cùng gốc tọa độ. Biết trong quá trình dao động, khoảng cách giữa hai vật lớn nhất bằng 10 cm và vận tốc tương đối giữa chúng có độ lớn cực đại bằng 1 m/s. Để hai con lắc trên dừng lại thì phải thực hiện lên hệ hai con lắc một công cơ học có tồng độ lớn bằng
A. 0,25 J
B. 0,50 J
C. 0,15 J
D. 0,1 J


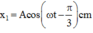
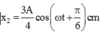

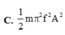
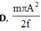
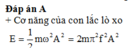
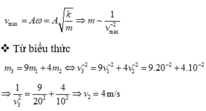

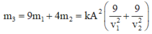


Chọn đáp án A.
Ta có:
Δ x m a x = 10 c m
= A 2 + ( 3 A / 4 ) 2 - 2 A . 3 A / 4 . cos ( π 6 + π 2 )
=> A = 8 cm (1)
Lại có: v 1 = - W . A . sin ( f t + π 3 )
và v 2 = - W . 3 A / 4 . sin ( f t + π 6 )
mà: v 1 - v 2 m a x = 1 m / s
=> 1 = ( W A ) 2 + ( 3 W A / 4 ) 2
=> WA = 0,8 m/s , kết hợp với (1)
=> W = 10 rad/s .
-Biên độ của hai con lắc lần lượt là: A 1 = A 2 = 8 c m
Và A 2 = 30 4 = 6 c m
+ Công cần thiết tác dụng vào hai con lắc để 2 con lắc đứng yên bằng tổng năng lượng của hai con lắc:
A t d = W 1 + W 2 = 1 2 m w 2 A 1 2 + 1 2 m w 2 A 2 2 = 1 2 m x 2 ( A 1 2 + A 2 2 )
=0,25J