Hai điểm A và B cách nhau 40cm, nằm trên cùng một bán kính của một đĩa tròn, phẳng, mỏng quay đều quanh một trục qua tâm và vuông góc vói mặt đĩa. Điểm A có tốc độ dài 1,2m/s, còn điểm B có tốc độ dài 0,4m/s. Tốc độ góc của đĩa và khoảng cách từ điểm B đến trục quay lần lượt là A. 2rad/s và 20cm B. 1rad/s và 20cm C. 3rad/s và 60cm D. 4rad/s và 20cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tốc độ góc của điểm A và điểm B bằng nhau: ω A = ω B
Tốc độ dài của điểm A và điểm B khác nhau:
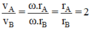
Gia tốc hướng tâm của điểm A và điểm B khác nhau:
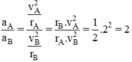

Chọn C.
Tốc độ góc ω = 50.2π /20= 5π rad/s
Tốc độ dài của điểm ở mép đĩa: v = ωr = 5π.0,5 ≈ 7,85 m/s.

Chọn đáp án C
+ Chu kì quay của đĩa: ![]()
+ Tốc độ góc: ![]()
+ Tốc độ dài: ![]()

Chọn C.
Tốc độ góc
ω = 50 . 2 π 20 = 5 π rad / s
Tốc độ dài của điểm ở mép đĩa: v = ωr = 5π.0,5 ≈ 7,85 m/s.

Chọn đáp án C
+ Tốc độ góc: 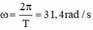
+ Tốc độ dài: ![]()
+ Gia tốc hướng tâm: ![]()

A và B có cùng tốc độ góc \(\omega\)
\(r_A;r_B\) là bán kính quỹ đạo chuyển dộng tròn đều của A và B.
Ta có: \(r_A-r_B=40\) (1)
Tốc độ dài của A và B:
\(\left\{{}\begin{matrix}v_A=\omega\cdot r_A=1,2\\v_B=\omega\cdot r_B=0,4\end{matrix}\right.\)\(\Rightarrow r_A=3r_B\left(2\right)\)
Từ (1) và (2) ta suy ra: \(r_B=20cm\)
\(\omega=\dfrac{v_B}{r_B}=\dfrac{0,4}{20\cdot10^{-2}}=2\)rad/s
Chọn A.