Một vật khối lượng 500 kg móc ở đầu sợi dây cáp của một cần cẩu và được kéo thẳng đứng từ mặt đất lên phía trên với sức căng không đổi. Khi tới độ cao 4,5 m thì vật đạt được vận tốc 0,60 m/s. Xác định lực căng của sợi dây cáp. Lấy g = 9,8 m/ s 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
31 tháng 7 2019
Nếu dây cáp chịu được lực căng tối đa T m a x = 6000 N > 4920 N, thì ở cùng độ cao nêu trên vật có thể đạt được vận tốc tối đa v m a x sao cho :
m v m a x 2 /2 + mgh = T m a x h
VT
29 tháng 8 2018
Vật chịu tác dụng của hai lực: lực căng T → của sợi dây cáp hướng thẳng đứng lên phía trên, trọng lực P → hướng thẳng đứng xuống phía dưới. Chọn chiều chuyển động của vật là chiều dương.
Áp dụng định luật II Niu-tơn đối với chuyển động của vật :
ma = P - T = mg - T
suy ra lực căng của sợi dây cáp : T = m(g - a). Do đó, công thực hiện bởi lực căng :
A 1 = -Ts = -ms(g - a) = -50.20.(9,8 - 2,5) = -7,3 kJ
VT
16 tháng 9 2019
Vật chịu tác dụng của hai lực: lực căng T → của sợi dây cáp hướng thẳng đứng lên phía trên, trọng lực P → hướng thẳng đứng xuống phía dưới. Chọn chiều chuyển động của vật là chiều dương.
Công thực hiện bởi trọng lực tác dụng lên vật:
A 2 = Ps = mgs = 50.9,8.20 = 9,8 kJ
VT
20 tháng 9 2017
Vật chịu tác dụng của hai lực: lực căng T → của sợi dây cáp hướng thẳng đứng lên phía trên, trọng lực P → hướng thẳng đứng xuống phía dưới. Chọn chiều chuyển động của vật là chiều dương.
Áp dụng công thức về độ biến thiên động năng :
Thay v 0 = 0 và A = A 1 + A 2 , ta tìm được động năng của vật ở cuối đoạn dịch chuyển :
m v 2 /2 = A 1 + A 2 = -7,3 + 9,8 = 2,5(kJ)
VT
26 tháng 4 2017
a. Chọn mốc thế năng tại vị trí cân bằng
W H = W A ⇒ 1 2 m v H 2 = m g z A ⇒ z A = v H 2 2 g = ( 2 2 ) 2 2.10 = 0 , 4 ( m )
Mà z A = l − l cos α 0 ⇒ 0 , 4 = 0 , 8 − 0 , 8. cos α 0 ⇒ cos α 0 = 1 2 ⇒ α 0 = 60 0
Vậy vật có độ cao z= 0,4 m so với vị trí cân bằng và dây hợp với phương thẳng đứng một góc 60 0
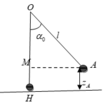
b. Theo điều kiện cân bằng năng lượng
W A = W B m g z A = m g z B + 1 2 m v B 2 ⇒ 10.0 , 4 = 10.0 , 8 ( 1 − c o s 30 0 ) = 1 2 v B 2 ⇒ v B = 2 , 42 ( m / s )
Xét tại B theo định luật II Newton
P → + T → = m a →
Chiếu theo phương của dây
− P cos α + T = m v B 2 l ⇒ − 0 , 2.10. cos 30 0 + T = 0 , 2. 2 , 42 2 0 , 8 ⇒ T = 3 , 2 ( N )
c. Gọi C là vị trí để vật có vận tốc 2 ( m / s ) .
Theo định luật bảo toàn cơ năng
W A = W C ⇒ m g z A = 1 2 m v C 2 + m g z B ⇒ g z A = 1 2 v C 2 + g z C ⇒ 10.0 , 4 = 1 2 . ( 2 ) 2 + 10. z C ⇒ z C = 0 , 3 ( m )
Mà z C = l − l cos α C ⇒ cos α C = 5 8 ⇒ α C = 51 , 32 0
Xét tại C theo định luật II Newton P → + T → = m a →
Chiếu theo phương của dây
− P cos α C + T C = m v C 2 l ⇒ − 0 , 2.10. 5 8 + T C = 0 , 2. ( 2 ) 2 0 , 8 ⇒ T = 1 , 75 ( N )
d. Gọi D là vị trí để W d = 3 W t . Theo định luật bảo toàn cơ năng
W A = W D ⇒ m g z A = W dD + W t D ⇒ m g z A = 4 3 W dD ⇒ g z A = 4 3 . 1 2 v D 2 ⇒ 10.0 , 4 = 4 6 . v D 2 ⇒ v D = 6 ( m / s )
Mà v D = 2 g l ( cos α D − cos 60 0 ) ⇒ 6 = 2.10.0 , 8 ( cos α D − 0 , 5 ) ⇒ cos α D = 7 8
Xét tại D theo định luật II Newton P → + T → = m a →
Chiếu theo phương của dây
− P cos α D + T D = m v D 2 l ⇒ − 0 , 2.10. 7 8 + T D = 0 , 2. ( 6 ) 2 0 , 8 ⇒ T = 3 , 25 ( N )
Vật nặng chịu lực căng T → (ngoại lực) tác dụng, chuyển động từ mặt đất lên tới độ cao h = 10 m và đạt được vận tốc v = 0,5 m. Trong trường hợp này, độ biến thiên cơ năng của vật có giá trị bằng công do ngoại lực thực hiện, nên ta có :
m v 2 /2 + mgh = Th
suy ra lực căng của sợi dây cáp :
T = m( v 2 /2h + g) ≈ 500(4,5. 0 , 6 2 /2 + 9,8) = 4920(N)