Giả sử AB là một dây cung của đường tròn (O). Trên cung nhỏ AB lấy các điểm C và D sao cho A C ⏜ = B D ⏜ . Chứng minh AB và CD song song
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 11 2019
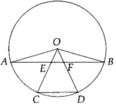
a, Chứng minh được ∆OEA = ∆OFB => AE = FB
b, Chứng minh được O E F ^ = O C D ^ => AB//CD
CH
Cô Hoàng Huyền
Admin
VIP
30 tháng 1 2018
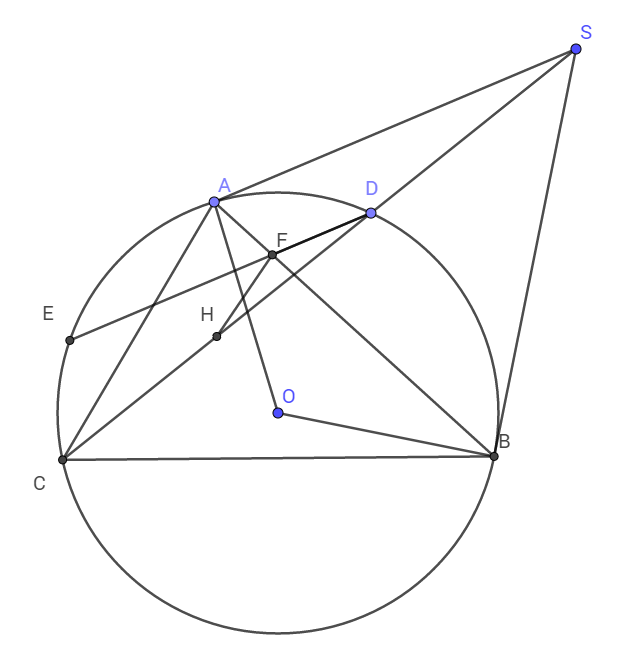
Ta có các tam giác vuông AOS; HOS, BOS có chung cạnh huyền OS nên S, A, H, O, B nội tiếp đường tròn đường kính OS.
Khi đó ta có :
\(\widehat{ASH}=\widehat{ABH}\) (Hai góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{ASH}=\widehat{FDH}\) (Hai góc đồng vị)
\(\Rightarrow\widehat{ABH}=\widehat{FDH}\)
Suy ra tứ giác HFDO nội tiếp.
Từ đó ta có \(\widehat{FHD}=\widehat{ABD}\)(Hai góc nội tiếp)
Mà \(\widehat{ABD}=\widehat{ACD}\) (Hai góc nội tiếp)
Nên \(\widehat{FHD}=\widehat{ACD}\)
Chúng lại ở vị trí đồng vị nên HF // AC.
NM
Nguyễn Minh Quang
Giáo viên
7 tháng 1 2021
do AB//CD nên ta có số đo cung AC=BD
mà \(\widehat{AMC}=\frac{1}{2}sd\widebat{AC}=\frac{1}{2}sd\widebat{BD}=\widehat{BMD}\)
Ta lấy K là điểm chính giữa cung nhỏ A B ⏜
Ta chứng minh được C K ⏜ = K D ⏜
Từ đó ta có OK ⊥ CD, OK ⊥ AB => CD//AB