Cho hàm số f(x)=a x 2 -2(a+1)x+a+2 (a ≠ 0)
Chứng tỏ rằng phương trình f(x)=0 luôn có nghiệm thực. Tính các nghiệm đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
6 tháng 12 2018
Đúng(0)
Những câu hỏi liên quan
2 tháng 4 2017
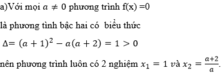
Ta có:
f(x) = ax2 – 2(a + 1)x + a + 2 = (x – 1)(ax – a- 2) nên phương trình f(x) = 0 luôn có hai nghiệm thực là:
x = 1, x=a+2ax=a+2a
Theo định lí Vi-et, tổng và tích của các nghiệm đó là:
S=2a+2a,P=a+2aS=2a+2a,P=a+2a
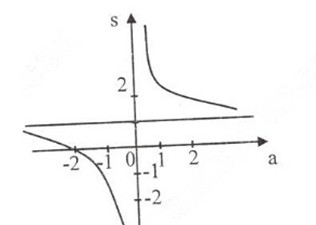
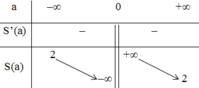
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số S=2a+2a=2+2aS=2a+2a=2+2a
- Tập xác định : (-∞, 0)∪ (0, +∞)
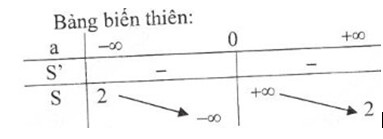
- Sự biến thiên: S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞)S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞) nên hàm số nghịch biến trên hai khoảng (-∞, 0) và (0, +∞)
- Cực trị: Hàm số không có cực trị
- Giới hạn tại vô cực và tiệm cận ngang
lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2
Vậy S = 2 là tiệm cận ngang
- Giới hạn vô cực và tiệm cận đứng:
lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞
Vậy a = 0 là tiệm cận đứng.
- Bảng biến thiên:
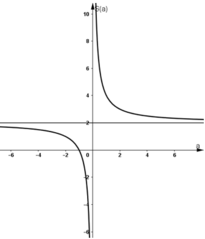
Đồ thị hàm số:
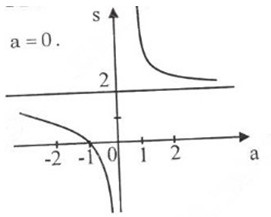
Đồ thị không cắt trục tung, cắt trục hoành tại a = -1
2) Khảo sát sự biến thiên và vẽ đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a
Tập xác định: D = R\{0}
S′=−2a2<0,∀a∈DS′=−2a2<0,∀a∈D
lima→0−S=−∞lima→0−S=−∞⇒ Tiệm cận đứng: a = 0
lima→±∞S=1lima→±∞S=1⇒ Tiệm cận ngang: S = 1
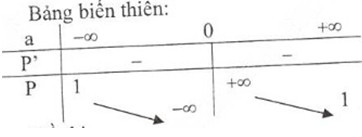
Đồ thị hàm số:
Ngoài ra: đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a có thể nhận được bằng cách tịnh tiến đồ thị S=2a+2a=2+2aS=2a+2a=2+2a dọc theo trục tung xuống phía dưới 1 đơn vị.
CM
3 tháng 1 2019
Chọn C.
- Hàm số g(x) = f(x) - x xác định và liên tục trên đoạn [a ; b].
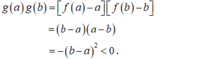
- Suy ra: phương trình f(x) – x = 0 luôn có nghiệm trên khoảng (a, b).
CM
30 tháng 10 2017
Vì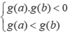 
Do đó đường thẳng y = 0 cắt đồ thị hàm số g(x) tại ba điểm phân biệt có hoành độ 
Vì vậy g(f(x)0 
Hàm số f(x) có 
đồng biến trên R do đó mỗi phương trình 
có một nghiệm thực duy nhất.
Vậy phương trình đã cho có 3 nghiệm thực.
Chọn đáp án A.
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2022
2.
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(x+2a\right)=2a\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\left(x^2+x+1\right)=1\)
Hàm liên tục tại \(x=0\Leftrightarrow\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^+}f\left(x\right)\)
\(\Leftrightarrow2a=1\Rightarrow a=\dfrac{1}{2}\)
3. Đặt \(f\left(x\right)=x^4-x-2\)
Hàm \(f\left(x\right)\) liên tục trên R nên liên tục trên \(\left(1;2\right)\)
\(f\left(1\right)=-2\) ; \(f\left(2\right)=12\Rightarrow f\left(1\right).f\left(2\right)=-24< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc (1;2)
Hay pt đã cho luôn có nghiệm thuộc (1;2)
CM
29 tháng 9 2018
Bảng biến thiên:
Đồ thị ( hình thang trên ).
* Khảo sát hàm số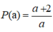 
+ Tập xác định: D = R\{0}.
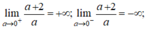
⇒ Đường thẳng a = 0 là tiệm cận đứng của đồ thị hàm số.
+ Lại có: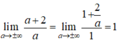 
Do đó, đường thẳng P(a) =1 là tiệm cận ngang của đồ thị hàm số.
+ Đạo hàm: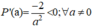 
Do đó hàm số này nghịch biến trên tập xác định.
Bảng biến thiên
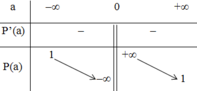
Đồ thị hàm số
CM
12 tháng 6 2017
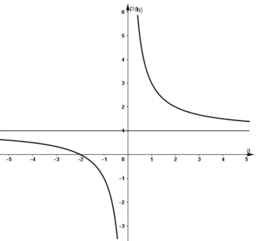
Xét hàm số g(x) = f(x) − f(x + 0,5)
Ta có
g(0) = f(0) − f(0 + 0,5) = f(0) − f(0,5)
g(0,5) = f(0,5) − f(0,5 + 0,5) = f(0,5) − f(1) = f(0,5) − f(0)
(vì theo giả thiết f(0) = f(1)).
Do đó,
g ( 0 ) . g ( 0 , 5 ) = [ f ( 0 ) − f ( 0 , 5 ) ] . [ f ( 0 , 5 ) − f ( 0 ) ] = − f ( 0 ) − f ( 0 , 5 ) 2 ≤ 0 .
- Nếu g(0).g(0,5) = 0 thì x = 0 hay x=0,5 là nghiệm của phương trình g(x) = 0
- Nếu g(0).g(0,5) < 0 (1)
Vì y = f(x) và y = f(x + 0,5) đều liên tục trên đoạn [0; 1] nên hàm số y = g(x) cũng liên tục trên [0; 1] và do đó nó liên tục trên [0; 0,5] (2)
Từ (1) và (2) suy ra phương trình g(x) = 0 có ít nhất một nghiệm trong khoảng
Kết luận : Phương trình g(x) = 0 hay f(x) − f(x + 0,5) = 0 luôn có nghiệm trong đoạn (0;0,5)
