Giải phương trình: z - i 2 + 4 = 0 trên tập số phức.
(Đề thi tốt nghiệp THPT năm 2011)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(1 − i)z + (2 − i) = 4 − 5i
⇔ (1 − i)z = 4 − 5i – 2 + i
⇔(1 − i)z = 2 − 4i
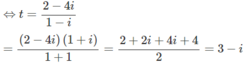

(1 − i)z + (2 − i) = 4 − 5i
⇔ (1 − i)z = 4 − 5i – 2 + i
⇔(1 − i)z = 2 − 4i
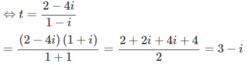

TXĐ: D = R
y’ = 3 x 2 – 4x + m; y’ = 0 ⇔ 3 x 2 – 4x + m = 0
Phương trình trên có hai nghiệm phân biệt khi:
∆ ’ = 4 – 3m > 0 ⇔ m < 4/3 (∗)
Hàm số có cực trị tại x = 1 thì :
y’(1) = 3 – 4 + m = 0 ⇒ m = 1 (thỏa mãn điều kiện (∗) )
Mặt khác, vì:
y’’ = 6x – 4 ⇒ y’’(1) = 6 – 4 = 2 > 0
cho nên tại x = 1, hàm số đạt cực tiểu.
Vậy với m = 1, hàm số đã cho đạt cực tiểu tại x = 1

TXĐ: D = R
y’ = 3 x 2 – 4x + m; y’ = 0 ⇔ 3 x 2 – 4x + m = 0
Phương trình trên có hai nghiệm phân biệt khi:
∆’ = 4 – 3m > 0 ⇔ m < 4/3 (∗)
Hàm số có cực trị tại x = 1 thì :
y’(1) = 3 – 4 + m = 0 ⇒ m = 1 (thỏa mãn điều kiện (∗) )
Mặt khác, vì:
y’’ = 6x – 4 ⇒ y’’(1) = 6 – 4 = 2 > 0
cho nên tại x = 1, hàm số đạt cực tiểu.
Vậy với m = 1, hàm số đã cho đạt cực tiểu tại x = 1

a) TXĐ: D = R
Sự biến thiên:
y′ = 3 x 2 – 6x = 3x(x – 2)
y′=0 ⇔ 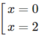
Hàm số đồng biến trên mỗi khoảng (– ∞ ;0), (2;+ ∞ )
Hàm số nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại x = 0 ; y C Đ = y(0) = 0
Hàm số đạt cực tiểu tại x = 2; y C T = y(2) = -4.
Giới hạn: 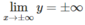
Điểm uốn: y” = 6x – 6, y” = 0 ⇔ x = 1; y(1) = –2
Suy ra đồ thị có điểm uốn I(1; -2)
Bảng biến thiên:
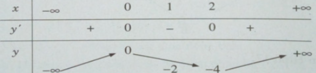
Đồ thị:
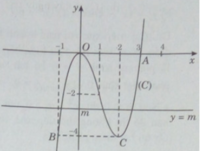
Đồ thị cắt trục hoành tại O(0;0), A(3;0). Đồ thị đi qua điểm B(-1;-4); C(2;-4).
b) x 3 – 3 x 2 – m = 0 ⇔ x 3 – 3 x 2 = m x 3 – 3 x 2 – m = 0 ⇔ x 3 – 3 x 2 = m (∗)
Phương trình (∗) có 3 nghiệm phân biệt khi và chỉ khi đường thẳng y = m cắt (C) tại 3 điểm phân biệt. Từ đó suy ra: – 4 < m < 0.

Chọn D.
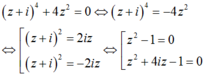
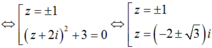
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
z - i 2 + 4 = 0
⇔ z - i 2 = −4