Một đoàn tàu bắt đầu rời ga và chuyển động thẳng nhanh dần đều. Sau khi chạy được 1,5 km thì đoàn tàu đạt vận tốc 36 km/h. Tính vận tốc của đoàn tàu sau khi chạy được 3 km kể từ khi đoàn tàu bắt đầu rời ga.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 8 2017
Ta có
2as1 = v12 - v02
Theo đề bài v0 = 0(km/h)
=> 2as1 = v12
Tương tự :
2as2 = v22
<=> \(\dfrac{s_1}{s_2}=\dfrac{v_1^2}{v_2^2}\)
<=> \(\dfrac{1}{3}=\dfrac{36^2}{v_2^2}\)
<=> v2 = 62,4(km/h)
11 tháng 10 2021
\(v=144\)km/h=40m/s
a) Gia tốc tàu: \(v^2-v_0^2=2aS\)\(\Rightarrow\) \(40^2-0=2a\cdot200\Rightarrow a=4\)m/s2
b) \(v'=360\)km/h=100m/s
Thời gian tàu đi đc khi đó: \(v'=v_0+at\Rightarrow100=0+4\cdot t\Rightarrow t=25s\)
25 tháng 9 2016
a) Áp dụng công thức liên hệ ta có:
\(v^2-v0^2=2as\Leftrightarrow400-0=2\cdot200a\Leftrightarrow a=1\)
b) Áp dụng công thức: v=v0+at ta có:
20=0+1*a\(\Leftrightarrow\)a=20s
23 tháng 9 2021
a) Đổi 36km/h = 10m/s
Gia tốc của tàu:
Ta có: \(v=v_0+at\Leftrightarrow a=\dfrac{v-v_0}{t}=\dfrac{10-0}{20}=0,5\left(m/s^2\right)\)
b) Đổi 54km/h = 15m/s
Thời gian để vật đạt đến vận tốc đó:
Ta có: \(v=v_0+at\Leftrightarrow t=\dfrac{v-v_0}{a}=\dfrac{15-0}{0,5}=30\left(s\right)\)
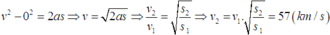
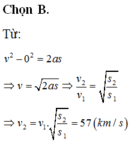
Công thức độc lập với thời gian trong chuyển động thẳng nhanh dần đều là: v 2 - v 0 2 = 2as
Gọi v 1 là vận tốc của đoàn tàu sau khi đi được đoạn đường s 1 = 1,5 km và v 2 là vận tốc của đoạn tàu sau khi chạy được đoạn đường s 2 = 3 km kể từ khi đoàn tàu bắt đầu rời ga.
Vì gia tốc a không đổi và vận tốc ban đầu v 0 = 0, nên ta có: v 1 2 = 2as1; v 2 2 = 2a s 2
Do đó