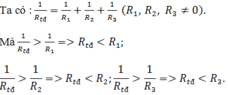Cho đoạn mạch gồm hai điện trở R1 và R2 mắc song song nhau, điện trở tương đương Rtđ = 10 _ , biết điện trở R1 = 120.Tính điện trở R2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



tóm tắc
\(R_1=R_2=6\left(\text{ Ω}\right)\)
\(R_{tđ}=?\)
Giải
Điện trở tương đương của đoạn mạch là:
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Rightarrow R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{6.6}{6+6}=3\left(\text{Ω}\right)\)
Đáp số : \(R_{tđ}=3\text{Ω}\)

\(R_1//R_2\)\(\Rightarrow\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Rightarrow\dfrac{1}{2,4}=\dfrac{1}{6}+\dfrac{1}{R_1}\)
\(\Rightarrow R_1=4\Omega\)
Ta có \(R_{td}=\dfrac{R_1R_2}{R_1+R_2}\) \(\Leftrightarrow2,4=\dfrac{R_16}{R_1+6}\Leftrightarrow2,4\left(R_1+6\right)=6R_1\)
\(\Leftrightarrow2,4R_1+14,4=6R_1\Leftrightarrow-3,6R_1=-14,4\Rightarrow R_1=4\Omega\)

R1//R2
a, =>\(Rtd=\dfrac{R1R2}{R1+R2}=\dfrac{20.20}{20+20}=10\left(ôm\right)\)
b,R1//R2//R3
\(=>\dfrac{1}{Rtd}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=\dfrac{1}{20}+\dfrac{1}{20}+\dfrac{1}{15}=>Rtd=6\left(ôm\right)\)c,
=>U1=U2=U3=30V
\(=>I1=\dfrac{U1}{R1}=\dfrac{30}{20}=1,5A,=>I2=\dfrac{U2}{R2}=1,5A\)
\(=>I3=\dfrac{U3}{R3}=2A\)
\(=>Im=\dfrac{U}{Rtd}=\dfrac{30}{6}=5A\)

Công thức tính điện trở tương đương đối với:
Đoạn mạch gồm hai điện trở R1 và R2 mắc nối tiếp: Rtđ = R1 + R2
Đoạn mạch gồm hai điện trở R1 và R2 mắc song song.
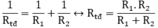

Do mắc song song nên:
\(R_{tđ}=\dfrac{1}{\dfrac{1}{R_1}+\dfrac{1}{R_2}}\)\(\Rightarrow1=\dfrac{1}{\dfrac{1}{3}+\dfrac{1}{R_2}}\)
\(\Rightarrow\dfrac{1}{3}+\dfrac{1}{R_2}=1\Rightarrow\dfrac{1}{R_2}=\dfrac{2}{3}\Rightarrow R_2=1,5\left(\Omega\right)\)

a. \(\dfrac{1}{R}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{30}=\dfrac{1}{5}\Rightarrow R=5\Omega\)
b. \(U=U1=U2=U3=R1.I1=10.0,3=3V\)(R1//R2//R3)
c. \(\left\{{}\begin{matrix}I2=U2:R2=3:15=0,2A\\I3=U3:R3=3:30=0,1A\\I=U:R=3:5=0,6A\end{matrix}\right.\)