Chứng minh rằng: 10 1 + 10 100 - 1 - 10 100 là một số nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
30 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
LT
3 tháng 4 2017
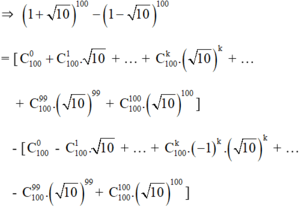
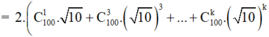
a) 1110 – 1 = (1 + 10)10 – 1 = (1 + C110 10 + C210102 + … +C910 109 + 1010) – 1
= 102 + C210102 +…+ C910 109 + 1010.
Tổng sau cùng chia hết cho 100 suy ra 1110 – 1 chia hết cho 100.
b) Ta có
101100 – 1 = (1 + 100)100 - 1
= (1 + C1100 100 + C2100 1002 + …+C99100 10099 + 100100) – 1.
= 1002 + C21001002 + …+ 10099 + 100100.
Tổng sau cùng chia hết cho 10 000 suy ra 101100 – 1 chia hết cho 10 000.
c) (1 + √10)100 = 1 + C1100 √10 + C2100 (√10)2 +…+ (√10)99 + (√10)100
(1 - √10)100 = 1 - C1100 √10 + C2100 (√10)2 -…- (√10)99 + (√10)100
√10[(1 + √10)100 – (1 - √10)100] = 2√10[C1100 √10 + C3100 (√10)3 +…+ . (√10)99]
= 2(C1100 10 + C3100 102 +…+ 1050)
Tổng sau cùng là một số nguyên, suy ra √10[(1 + √10)100 – (1 - √10)100] là một số nguyên.
BT
23 tháng 5 2017
a) \(11^{10}-1=\left(10+1\right)^{10}-1\)\(=C^0_{10}10^{10}+C^1_{10}10^9+...+C^9_{10}10+C^{10}_{10}-1\)
\(=10^{10}+C^1_{10}10^9+...+C^8_{10}10^2+10.10\) chia hết cho 100.
b) \(\left(101\right)^{100}-1=\left(100+1\right)^{100}-1\)
\(=100^{100}+C_{100}^{99}100^{99}+....+C^1_{100}100+C_{100}^{100}100^0-1\)
\(=100^{100}+C_{100}^{99}100^{99}+....+C^2_{100}100^2+100.100+1-1\)
\(=100^{100}+C_{100}^{99}100^{99}+....+C^2_{100}100^2+10000\) chia hết cho 10000.
DD
3
NC
0
17 tháng 10 2019
\(10^{100}+10^{51}+25=\left(10^{50}\right)^2+10\cdot10^{50}+25\)
\(=\left(10^{50}\right)^2+2\cdot10^{50}+5+5^2=\left(10^{50}+5\right)^2\)là SCP (Đpcm)
24 tháng 3 2020
1110-1=(11-1)(119+118+...+11)=10(119+118+...+11)⋮10
Vì 1110-1⋮10=>11x-1⋮10<=>(119+118+...+11)⋮10
=>10(119+118+...+11)⋮100
=>1110-1⋮100
29 tháng 6 2020
Ta có:\(\frac{1}{10}+\frac{1}{11}+...+\frac{1}{100}\)> \(\frac{1}{10}+\left(\frac{1}{100}+\frac{1}{100}+...+\frac{1}{100}\right)\)[ 90 p/s \(\frac{1}{100}\)]
= \(\frac{1}{10}+\frac{90}{100}=\frac{10}{100}+\frac{90}{100}\)=\(\frac{100}{100}=1\)
Vậy \(\frac{1}{10}+\frac{1}{11}+...+\frac{1}{100}\)>1
\(\frac{1}{10}+\frac{1}{11}+...+\frac{1}{100}\)\(\frac{1}{10}+\frac{1}{11}+...+\frac{1}{100}\)
NH
1
