Cho hình thang ABCD có hai đáy AB, CD và AB < CD. Khẳng định nào sau đây là đúng?
A. A B → c ù n g h ư ớ n g v ớ i C D →
B. A D → c ù n g h ư ớ n g v ớ i B C →
C. A B → n g ư ợ c h ư ớ n g v ớ i C D →
D. A D → n g ư ợ c h ư ớ n g v ớ i B C →
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Vì ABCD là hình thang vuông tại A, D
⇒ A D ⊥ C D .
Mà S A ⊥ A B C D ⇒ S A ⊥ S A D ⇒ C D ⊥ S D
⇒ Tam giác SCD vuông tại D
Vì E là trung điểm của AB suy ra AECD là hình vuông
⇒ C E ⊥ A B mà S A ⊥ A B C D ⇒ S A ⊥ A B
suy ra C E ⊥ S A B

Chọn B.
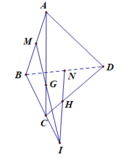
M G ⊂ A B C N H ⊂ B C D A B C ∩ B C D = B C N H ∩ M G = I ⇒ I ∈ B C
vậy B, I, C thẳng hàng

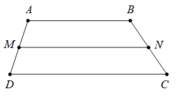
Vì M; N lần lượt là trung điểm của AD; BC
M A → + M D → = 0 → B N → + C N → = 0 → .
Dựa vào đáp án, ta có nhận xét sau:
A đúng, vì :
M D → + C N → + D C → = M N → = M D → + D C → + C N → = M C → + C N → = M N → .
B đúng, vì A B → − M D → + B N → = A B → + B N → − M D → = A N → − A M → = M N → .
C đúng, vì M N → = M A → + A B → + B N → và M N → = M D → + D C → + C N → .
Suy ra
2 M N → = M A → + M D → + A B → + D C → + B N → + C N → = 0 → + A B → + D C → + 0 → = A B → + D C →
⇒ M N → = 1 2 A D → + B C → .
D sai, vì theo phân tích ở đáp án C.
Chọn D.

*Xét tam giác ABC có M; N là trung điểm của AB, BC nên MN là đường trung bình của tam giác.
⇒ M N / / A C ; M N = 1 2 A C ( 1 )
* Xét tam giác ADC có P; Q là trung điểm của CD, DA nên PQ là đường trung bình của tam giác.
⇒ P Q / / A C ; P Q = 1 2 A C ( 2 )
* Từ (1) (2) suy ra PQ// MN; PQ = MN.
Khi đó M N → = Q P →
Đáp án D
Theo tính chất của hình thang và cách đánh số đỉnh hình thang, hai đỉnh B, D nằm khác phía với đường thẳng AC, do đó A B → v à C D → ngược hướng.
AB < CD nên ABCD không là hình bình hành.
Đáp án C.