Một điểm M thuộc parabol (P): y 2 = x. Nếu khoảng cách từ M đến tiêu điểm F của (P) bằng 1 thì hoành độ của điểm M bằng bao nhiêu?
A. 3/4
B. 3 /2
C. 3
D. 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi parabol có dạng y=ax2
Vì P đi qua A(-2;-2)\(\Rightarrow\)a=-\(\dfrac{1}{2}\)
\(\Rightarrow\)P có dạng y= -\(\dfrac{1}{2}\)x2 (1)
vì khoảng cách đến trục hoành gấp đôi khoảng cách đến trục tung\(\Rightarrow\)\(\left|y\right|\)=2\(\left|x\right|\)
Nếu x>0 thì y>0 (vô lí)
Nếu x<0 thì y<0\(\Rightarrow\)y=-2x (2)
Từ (1) và (2) có x=4 và y=-2
hoặc x=-4 và y= -2
vậy M(4;-2) hoặc(-4;-2)

Đáp án: D
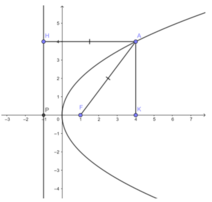
Ta có: (P) y 2 = 4x ⇒ F(1;0) ⇒ PF = 2
PK = AH = 5 ⇒ FK = 5 - 2 = 3
Mà AF = AH = 5
Xét tam giác vuông AKF có:
A K 2 = A F 2 - F K 2 = 5 2 - 3 2 = 16 ⇒ AK = 4
Vậy khoảng cách từ A đến trục hoành bằng 4

\(y'=4x^3-4mx\Rightarrow y'\left(1\right)=4-4m\)
\(A\left(1;1-m\right)\)
Phương trình tiếp tuyến d tại A có dạng:
\(y=\left(4-4m\right)\left(x-1\right)+1-m\)
\(\Leftrightarrow\left(4-4m\right)x-y+3m-3=0\)
\(d\left(B;d\right)=\dfrac{\left|\dfrac{3}{4}\left(4-4m\right)-1+3m-3\right|}{\sqrt{\left(4-4m\right)^2+1}}=\dfrac{1}{\sqrt{\left(4-4m\right)^2+1}}\le1\)
Dấu "=" xảy ra khi và chỉ khi \(4-4m=0\Rightarrow m=1\)
y′=4x3−4mx⇒y′(1)=4−4my′=4x3−4mx⇒y′(1)=4−4m
A(1;1−m)A(1;1−m)
Phương trình tiếp tuyến d tại A có dạng:
y=(4−4m)(x−1)+1−my=(4−4m)(x−1)+1−m
⇔(4−4m)x−y+3m−3=0⇔(4−4m)x−y+3m−3=0
d(B;d)=∣∣∣34(4−4m)−1+3m−3∣∣∣√(4−4m)2+1=1√(4−4m)2+1≤1d(B;d)=|34(4−4m)−1+3m−3|(4−4m)2+1=1(4−4m)2+1≤1
Dấu "=" xảy ra khi và chỉ khi 4−4m=0⇒m=1
Đáp án: A
(P): y 2 = x ⇒ p = 1/2
Ta có:
Hoành độ của điểm M chính là độ dài đoạn OK