Cho a là số thực dương. Biết rằng F(x) là một nguyên hàm của hàm số f x = e x ln a x + 1 x thỏa mãn F 1 a = 0 và F 2018 = e 2018 . Mệnh đề nào sau đây đúng?
A. a ∈ 1 2018 ; 1
B. a ∈ ( 0 ; 1 2018 ]
C. a ∈ [ 1 ; 2018 )
D. a ∈ [ 2018 ; + ∞ )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(F\left(x\right)=\int\left(e^x.ln\left(ax\right)+\dfrac{e^x}{x}\right)dx=\int e^xln\left(ax\right)dx+\int\dfrac{e^x}{x}dx=\int e^xlnxdx+\int\dfrac{e^x}{x}dx+\int e^x.lna.dx\)
Xét \(I=\int e^xlnxdx\)
Đặt \(\left\{{}\begin{matrix}u=lnx\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x}\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I=lnx.e^x-\int\dfrac{e^x}{x}dx\)
\(\Rightarrow F\left(x\right)=e^x.lnx+e^x.lna+C\)
\(F\left(\dfrac{1}{a}\right)=e^{\dfrac{1}{a}}ln\left(\dfrac{1}{a}\right)+e^{\dfrac{1}{a}}.lna+C=0\Rightarrow C=0\)
\(F\left(2020\right)=e^{2020}ln\left(2020\right)+e^{2020}.lna=e^{2020}\)
\(\Rightarrow ln\left(2020a\right)=1\Rightarrow a=\dfrac{e}{2020}\)

Chọn A
Đặt t = ln 2 x + 1 ⇒ t 2 = ln 2 x + 1 ⇒ t d t = ln x x d x
∫ ln 2 x + 1 . ln x x d x = ∫ t 2 d t = t 3 3 + C = ln 2 x + 1 3 3 + C
Vì F ( 1 ) = 1 3 nên C = 0
Vậy F 2 ( e ) = 8 9

Đáp án A
Phương pháp:
+) x e x là một nguyên hàm của hàm số nên x e x ' = f ( - x )
+) Từ f ( - x ) ⇒ f ( x )
+) F(x) là một nguyên hàm của f ' x e x ⇒ F ( x ) = ∫ f ' ( x ) e x d x
+) Tính F(x), từ đó tính F(-1)
Cách giải:
Vì x e x là một nguyên hàm của hàm số f ( - x ) nên x e x ' = f ( - x )
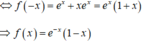
![]()
![]()
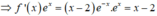
![]()
![]()
![]()
![]()
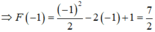

Chọn A
F ( x ) = ∫ 1 1 - 3 x + 1 d x = - 1 3 ∫ d ( 1 - 3 x ) 1 - 3 x + x = x - 2 3 1 - 3 x + C
F ( - 1 ) = 2 3 ⇒ C = 3 ⇒ F ( x ) = x - 2 3 1 - 3 x + 3
Đáp án A
Ta có: F x = ∫ e x ln a x + + 1 x d x = ∫ e x ln a x d x + ∫ e x x d x = I 1 + I 2
Tính I 2 = ∫ e x d x x ,đặt u = e x d v = 1 x d x ⇒ d u = e x d x v = ln x ⇒ I 2 = e x ln x - ∫ e x ln x d x
Do đó F x = e x ln x + ∫ e x ln a x - ln x d x = e x ln x + ∫ e x ln a d x = e x ln x + ln a + C = e x ln a x + C
Lại có : F 1 a = e 1 a ln 1 + C = 0 ⇒ C = 0 ; F 2018 = e 2018 ln 2018 a e 2018
Do đó ln 2018 a = 1 ⇒ a = e 2018 .