Cho hàm số : y = x 3 = 2018 x có đồ thị là (C) M là điểm trên (C) có hoành x 1 = 1 . Tiếp tuyến của (C) tại M cắt (C) tại điểm M 2 khác M 1 , tiếp tuyến của (C) tại M 2 cắt (C) tại điểm M 3 khác M 2 , tiếp tuyến của (C) tại điểm M n - 1 cắt (C) tại điểm M n khác M n - 1 n = 4 , 5 , . . . , gọi x n ; y n là tọa độ điểm M n . Tìm n để : 2018 x n + y n + 2 2019 = 0
A. n = 647
B. n = 675
C. n = 674
D. n = 627


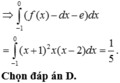

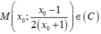 với
với 
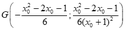
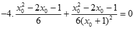
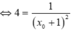
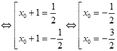

Đáp án C
Phương trình tiếp tuyến của (C) tại M k x k ; y k là y = y k = y ' x k x - x k
⇔ y = y ' x k x - x k + y k = 3 x k 2 - 2018 x - x k + x k 3 - 2018 x k ( d )
Phương trình hoành độ giao điểm của (C) và tiếp tuyến (d) là
x 3 - 2018 x = 3 x k 2 - 2018 x - x k + x k 3 - 2018 x k ⇔ x - x k x 2 + x k x - 2 x k 2 = 0 ⇔ [ x = x k x = - 2 x k Do đó x k + 1 = - 2 x k suy ra x 1 = 1 ; x 2 = - 2 ; x 3 = 4 ; . . . ; x n = ( - 2 ) n - 1 ( cấp số nhân với q = -2)
Vậy 2018 x n + y n + 2 2019 = 0 ⇔ x n 3 = - 2 2019 ⇔ - 2 3 n - 3 = - 2 2019 ⇒ n = 674