Chứng minh các đẳng thức sau:
a) 3 a 2 − 10 a + 3 2 ( a − 3 ) = 3 2 a − 1 2 với a ≠ 3;
b) b 2 + 3 b + 9 b 3 − 27 = b − 2 b 2 − 5 b + 6 với b ≠ 2 và b ≠ 3.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

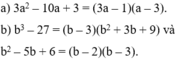

a) Ta có: \(\dfrac{3a^2-10a+3}{2\left(a-3\right)}\)
\(=\dfrac{3a^2-9a-a+3}{2\left(a-3\right)}\)
\(=\dfrac{3a\left(a-3\right)-\left(a-3\right)}{2\left(a-3\right)}\)
\(=\dfrac{\left(a-3\right)\left(3a-1\right)}{2\left(a-3\right)}\)
\(=\dfrac{3a-1}{2}\)
\(=\dfrac{3}{2}a-\dfrac{1}{2}\)(đpcm)
b) Ta có: \(\dfrac{b^2+3b+9}{b^3-27}\)\(=\dfrac{b^2+3b+9}{\left(b-3\right)\left(b^2+3b+9\right)}\)
\(=\dfrac{1}{b-3}\)
\(=\dfrac{b-2}{\left(b-3\right)\left(b-2\right)}\)
\(=\dfrac{b-2}{b^2-5b+6}\)(đpcm)

\(a,VT=\left(a^2+b^2\right)\left(c^2+d^2\right)=a^2c^2+b^2c^2+a^2d^2+b^2d^2\)
\(VP=\left(ac+bd\right)^2+\left(ad-bc\right)^2=a^2c^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2=a^2c^2+b^2c^2+a^2d^2+b^2d^2\)
\(\Rightarrow VT=a^2c^2+b^2c^2+a^2d^2+b^2d^2=VP\left(đpcm\right)\)
b, Tham khảo:Chứng minh hằng đẳng thức:(a+b+c)3= a3 + b3 + c3 + 3(a+b)(b+c)(c+a) - Hoc24

1) a³ + b³ + c³ - 3abc
=(a + b)(a² - ab + b²) + c³ - 3abc
=(a + b)(a² - ab + b²) + c(a² - ab + b²) - 2abc - ca² - cb²
=(a + b + c)(a² - ab + b²) - (abc + b²c + bc² + ac² + abc + c²a) + c³ + ac² + bc²
=(a + b = c)(a² - ab + b²) - (a + b + c)(bc + ca) + c²(a + b + c)
=(a + b + c)(a² + b² + c² - ab - bc - ca)
2) \(\left(3a+2b-1\right)\left(a+5\right)-2b\left(a-2\right)=\left(3a+5\right)\left(a-3\right)+2\left(7b-10\right)\left(1\right)\)
\(\Leftrightarrow3a^2+15a+2ab+10b-a-5-2ab+4b=3a^2+14a+15+14b-10\)
\(\Leftrightarrow3a^2+14a+14b-5=3a^2+14a+14b-5\)( đúng)
\(\Rightarrow\left(1\right)\) đúng (đpcm)

a: Ta có: \(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}}{2}-\dfrac{4\sqrt{6}}{2}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{-3}{2}\)

1) a3+b3+c3-3abc = (a+b)3-3ab(a+b)+c3-3abc
= (a+b+c)(a2+2ab+b2-ab-ac+c2) -3ab(a+b+c)
= (a+b+c)( a2+b2+c2-ab-bc-ca)

10. a) Ta có : (a + b)2 + (a – b)2 = 2(a2 + b2). Do (a – b)\(^2\) ≥ 0, nên (a + b)\(^2\) ≤ 2(a2 + b2).
b) Xét : (a + b + c)\(^2\) + (a – b)\(^2\) + (a – c)\(^2\) + (b – c)\(^2\)
. Khai triển và rút gọn, ta được : 3(a\(^2\) + b\(^2\) + c\(^2\)).
Vậy : (a + b + c)\(^2\) ≤ 3( a\(^2\) + b\(^2\) + c\(^2\)).
Cách khác : Biến đổi tương đương
a, \(\left(a+b\right)^2\le2\left(a^2+b^2\right)\)
\(\Leftrightarrow a^2+2ab+b^2\le2a^2+2b^2\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)luôn đúng
b, \(\left(a+b+c\right)^2\le3\left(a^2+b^2+c^2\right)\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2ac+2bc\le3a^2+3b^2+3c^2\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)(Luôn đúng)