Cho đường thẳng d: (m – 2)x + (m – 6 )y + m – 1 = 0. Khi m thay đổi thì đường thẳng d luôn đi qua điểm có tọa độ?
A. (3; 4)
B. (-2; 1)
C. 5 4 ; - 1 4
D. - 5 4 ; 1 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
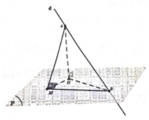
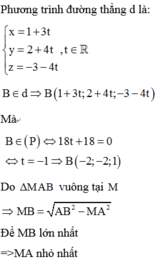
Gọi H là hình chiếu vuông góc của A lên mặt phẳng (P)
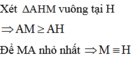
⇒ M B là giao tuyến của mặt phẳng (P) với mặt phẳng α ( α là mặt phẳng chứa d và vuông góc với mặt phẳng (P))
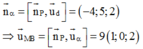
Vậy phương trình đường thẳng MB:
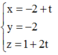
Thấy ngay điểm I(-1;-2;3) thỏa mãn.

Gọi \(A\left(x;y\right)\) là điểm cố định mà (d) luôn đi qua
\(\Rightarrow y=2mx+m+1\Rightarrow2mx+m+1-y=0\)
Vì khi m thay đổi thì (d) vẫn đi qua điểm A \(\Rightarrow\left\{{}\begin{matrix}x=0\\y=m+1\end{matrix}\right.\)
\(\Rightarrow\) (d) luôn đi qua điểm \(A\left(0,m+1\right)\)
Ta có (m – 2)x + (m – 6)y + m – 1 = 0 đúng với mọi m
⇔ mx - 2x + my - 6y + m – 1= 0 đúng với mọi m
⇔ (mx + my + m ) + ( -2x – 6y - 1)= 0 đúng với mọi m
⇔ m (x + y + 1) – (2x + 6y + 1) = 0 đúng với mọi m
Điểm cố định của d thỏa mãn
Đáp án D