Tính giá trị của B = x 2 + y 2 + z 2 ( y - z ) 2 + ( x - z ) 2 + ( x - y ) 2 . Biết x + y + z = 0.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
16 tháng 9 2018
Đúng(0)
Những câu hỏi liên quan
PN
0
NN
0
FF
2
S
2 tháng 12 2018
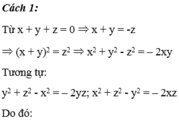
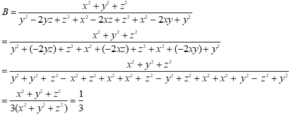
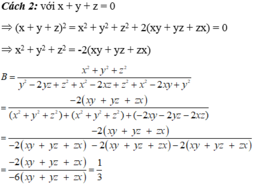
\(\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=1\Leftrightarrow\left(x+y+z\right)\left(\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}\right)=x+y+z\)
<=>\(\frac{x^2+x\left(y+z\right)}{y+z}+\frac{y^2+y\left(z+x\right)}{z+x}+\frac{z^2+z\left(x+y\right)}{x+y}=x+y+z\)
<=>\(\frac{x^2}{y+z}+x+\frac{y^2}{z+x}+y+\frac{z^2}{x+y}+z=x+y+z\)
<=>\(S=\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}=0\)
2 tháng 12 2018
x/(y+z)+y/(x+z)+z/(x+y)=1
=>\(\frac{x^2}{\left(y+z\right)^2}\)+\(\frac{y^2}{\left(x+z\right)^2}\)+\(\frac{z^2}{\left(x+y\right)^2}\)+2(\(\frac{xy}{\left(y+z\right)\cdot\left(x+z\right)}\)+\(\frac{yz}{\left(x+z\right)\left(x+y\right)}\)+\(\frac{zx}{\left(z+y\right)\cdot\left(x+y\right)}\))=1
PN
8 tháng 4 2016
\(a.\)
Phân tích biển đổi thành nhân tử kết hợp với chuyển vế để quy về hẳng đẳng thức, khi đó, ta tính được \(a,b\)
Thật vậy, ta có:
\(a^2-2a+6b+b^2=-10\)
\(\Leftrightarrow\) \(a^2-2a+6b+b^2+10=0\)
\(\Leftrightarrow\) \(\left(a^2-2a+1\right)+\left(b^2+6b+9\right)=0\)
\(\Leftrightarrow\) \(\left(a-1\right)^2+\left(b+3\right)^2=0\) \(\left(1\right)\)
Vì \(\left(a-1\right)^2\ge0;\) \(\left(b+3\right)^2\ge0\) với mọi \(a,b\)
nên để thỏa mãn đẳng thức \(\left(1\right)\) thì phải xảy ra đồng thời \(\left(a-1\right)^2=0\) và \(\left(b+3\right)^2=0\)
\(\Leftrightarrow\) \(a-1=0\) và \(b+3=0\) \(\Leftrightarrow\) \(a=1\) và \(b=-3\)
\(b.\) Cộng \(1\) vào mỗi phân thức của biểu thức \(A\), khi đó, ta có:
\(A+3=\left(\frac{x+y}{z}+1\right)+\left(\frac{x+z}{y}+1\right)+\left(\frac{y+z}{x}+1\right)=\frac{x+y+z}{z}+\frac{x+y+z}{y}+\frac{x+y+z}{x}\)
\(A+3=\left(x+y+z\right)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)=0\) (do \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\))
Vậy, \(A=-3\)
NC
1
AH
Akai Haruma
Giáo viên
3 tháng 2 2023
Lời giải:
Áp dụng BĐT Cô-si:
$\frac{1}{x(x+1)}+\frac{x}{2}+\frac{x+1}{4}\geq 3\sqrt[3]{\frac{1}{x(x+1)}.\frac{x}{2}.\frac{x+1}{4}}=\frac{3}{2}$
Tương tự:
$\frac{1}{y(y+1)}+\frac{y}{2}+\frac{y+1}{4}\geq \frac{3}{2}$
$\frac{1}{z(z+1)}+\frac{z}{2}+\frac{z+1}{4}\geq \frac{3}{2}$
Cộng theo vế các BĐT trên:
$\frac{1}{x^2+x}+\frac{1}{y^2+y}+\frac{1}{z^2+z}+\frac{3}{4}(x+y+z)+\frac{3}{4}\geq \frac{9}{2}$
$\frac{1}{x^2+x}+\frac{1}{y^2+y}+\frac{1}{z^2+z}+\frac{9}{4}+\frac{3}{4}\geq \frac{9}{2}$
$\Rightarrow \frac{1}{x^2+x}+\frac{1}{y^2+y}+\frac{1}{z^2+z}\geq \frac{3}{2}$
Vậy gtnn của biểu thức là $\frac{3}{2}$ khi $x=y=z=1$
5 tháng 12 2021
\(x^2+y^2-z^2=x^2+\left(y-z\right)\left(y+z\right)=x^2-x\left(y-z\right)=x\left(x-y+z\right)=x\left(-y-y\right)=-2xy\)
Tương tự \(x^2+z^2-y^2=-2xz;y^2+z^2-x^2=-2yz\)
Cộng VTV:
\(\Leftrightarrow\text{Biểu thức }=\dfrac{xy}{-2xy}+\dfrac{xz}{-2xz}+\dfrac{yz}{-2yz}=-\dfrac{1}{8}\)
