Thực hiện phép tính ( x 2 - x y ) 2 x 2 - y 2 . x + y x 3 y - x 2 y 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
15 tháng 11 2018
Đúng(0)
Những câu hỏi liên quan
17 tháng 2 2021
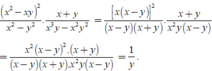
Ta có: \(\dfrac{y}{x-y}-\dfrac{x^3-xy^2}{x^2+y^2}\cdot\left(\dfrac{x}{x^2-2xy+y^2}-\dfrac{y}{x^2-y^2}\right)\)
\(=\dfrac{y}{x-y}-\dfrac{x\left(x^2-y^2\right)}{x^2+y^2}\cdot\left(\dfrac{x\left(x+y\right)}{\left(x-y\right)^2\cdot\left(x+y\right)}-\dfrac{y\cdot\left(x-y\right)}{\left(x-y\right)^2\cdot\left(x+y\right)}\right)\)
\(=\dfrac{y}{x-y}-\dfrac{x\left(x-y\right)\left(x+y\right)}{x^2+y^2}\cdot\dfrac{x^2+xy-xy+y^2}{\left(x-y\right)^2\left(x+y\right)}\)
\(=\dfrac{y}{x-y}-\dfrac{x\cdot\left(x^2+y^2\right)}{\left(x^2+y^2\right)\cdot\left(x-y\right)}\)
\(=\dfrac{y}{x-y}-\dfrac{x}{x-y}\)
\(=\dfrac{y-x}{x-y}=\dfrac{-\left(x-y\right)}{x-y}=-1\)
LN
3
KV
17 tháng 12 2020
MTC = (x - y)(x2 + xy + y2)
\(\dfrac{1}{x-y}-\dfrac{3xy}{x^3-y^3}+\dfrac{x-y}{x^2+xy+y^2}\)
\(=\dfrac{x^2+xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}-\dfrac{3xy}{\left(x-y\right)\left(x^2+xy+y^2\right)}+\dfrac{\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{x^2+xy+y^2-3xy+x^2-2xy+y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2x^2-4xy+2y^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x^2-2xy+y^2\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)
16 tháng 12 2020
1/x-y-3xy/x^3-y^3+x-y/x^2+xy+y^2
=1/x-y+-3xy/(x-y)(x^2+xy+y^2)+x-y/x^2+xy+y^2
=x^2+xy+y^2/(x-y)(x^2+xy+y^2)+-3xy/(x-y)(x^2+xy+y^2)+x^2-2xy+y^2/(x-y)(x^2+xy+y^2)
=x^2+xy+y^2-3xy+x^2-2xy-y^2/(x-y)(x^2+xy+y^2)
=2x^2-5xy/(x-y)(x^2+xy+y^2)
23 tháng 12 2021
a,\(\dfrac{x^2-9}{2x+6}:\dfrac{3-x}{2}=\dfrac{\left(x-3\right)\left(x+3\right)}{2\left(x+3\right)}.\dfrac{2}{3-x}=\dfrac{x-3}{3-x}=\dfrac{-\left(3-x\right)}{3-x}=-1\)
b, \(\dfrac{2x}{x-y}-\dfrac{2y}{x-y}=\dfrac{2x-2y}{x-y}=\dfrac{2\left(x-y\right)}{x-y}=2\)
23 tháng 12 2021
\(a,=\dfrac{\left(x-3\right)\left(x+3\right)}{2\left(x+3\right)}\cdot\dfrac{2}{-\left(x-3\right)}=\dfrac{x-3}{2}\cdot\dfrac{2}{-\left(x-3\right)}=-1\\ b,=\dfrac{2x-2y}{x-y}=\dfrac{2\left(x-y\right)}{\left(x-y\right)}=2\)
15 tháng 12 2020
Ta có:
\(\dfrac{1}{x-y}+\dfrac{3xy}{y^3-x^3}+\dfrac{x-y}{x^2+xy+y^2}\\ =\dfrac{x^2+xy+y^2-3xy+\left(x-y\right)^2}{x^3-y^3}\\ =\dfrac{2\left(x-y\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}\\ =\dfrac{2\left(x-y\right)}{x^2+xy+y^2}\)
15 tháng 12 2020
\(\dfrac{1}{x-y}+\dfrac{3xy}{y^3-x^3}+\dfrac{x-y}{x^2+xy+y^2}\) \(=\dfrac{x^2+xy+y^2}{x^3-y^3}-\dfrac{3xy}{x^3-y^3}+\dfrac{\left(x-y\right)^2}{x^3-y^3}\)
\(=\dfrac{x^2+xy+y^2-3xy+x^2-2xy+y^2}{x^3-y^3}\)
\(=\dfrac{2x^2+2y^2-4xy}{x^3-y^3}\)
\(=\dfrac{2x^2-2xy-2xy+2y^2}{x^3-y^3}\)
\(=\dfrac{2x\left(x-y\right)-2y\left(x-y\right)}{x^3-y^3}\)
\(=\dfrac{\left(2x-2y\right)\left(x-y\right)}{\left(x-y\right)\left(x^2+xy+y^2\right)}\)
\(=\dfrac{2x-2y}{x^2+xy+y^2}\)
