Tìm điều kiện của các biến để các phân thức sau có nghĩa - 5 x + 2 3 x + 2 2 x - 1 - 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
PT
1
CM
13 tháng 5 2018
Để phân thức có nghĩa:
x 2 + 5 x + 4 ≠ 0
⇔ (x + 4)(x + 1) ≠ 0
⇔ x ≠ -4, x ≠ -1
Vậy điều kiện để phân thức xác định là x ≠ -4 và x ≠ -1
GM
3
AT
14 tháng 7 2021
Để \(\sqrt{x^2+3}\) có nghĩa thì \(x^2+3\ge0\) (luôn đúng)
Để \(\sqrt{\left(x-1\right)\left(x+2\right)}\) có nghĩa thì \(\left(x-1\right)\left(x+2\right)\ge0\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1\ge0\\x+2\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1\le0\\x+2\le0\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le-2\end{matrix}\right.\)
14 tháng 7 2021
a) ĐKXĐ: \(x\in R\)
b) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\)
25 tháng 2 2021
a) ĐK: \(x-5\ne0\Leftrightarrow x\ne5\)
b)
ĐK: \(\left(\dfrac{1}{2}x+4\right)\ne0\Leftrightarrow\dfrac{1}{2}x\ne-4\\ \Leftrightarrow x\ne-8\)
c)ĐK:
\(-2x-10\ne0\\ \Leftrightarrow-2x\ne10\\ \Leftrightarrow x\ne-5\)
25 tháng 2 2021
a) ĐKXĐ: \(x\ne5\)
b) ĐKXĐ: \(x\ne-8\)
c) ĐKXĐ: \(x\ne-5\)
2 tháng 11 2021
Bài 5:
\(x^3=18+3\sqrt[3]{\left(9+4\sqrt{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\\ \Leftrightarrow x^3=18+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=18\\ y^3=6+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow y^3=6+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=6\\ P=x^3+y^3-3\left(x+y\right)+1993\\ P=\left(x^3-3x\right)+\left(y^3-3y\right)+1993\\ P=18+6+1993=2017\)
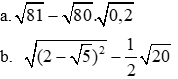
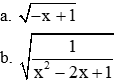
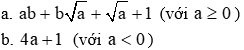
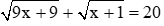
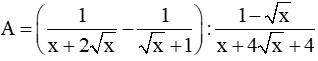
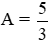
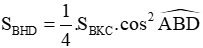
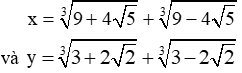
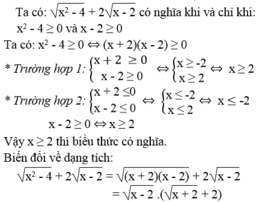
Để phân thức xác định ta có: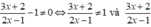
có nghĩa:
Vậy với x ≠ -3 và x ≠ ½ thì phân thức đã cho được xác định