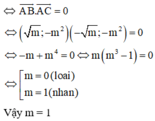Cho hàm số y = x 4 − 2 x 2 + m . Tìm các giá trị thực của m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác vuông cân.
A. m = 1
B. m = ± 1
C. m ∈ ℝ
D. m = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C

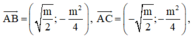
Tam giác ABC cân tại A, do đó để tam giác ABC vuông cân
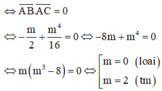

Hàm số có cực đại, cực tiểu khi m<2. Tọa độ các điểm cực trị là :
\(A\left(0;m^2-5m+5\right);B\left(\sqrt{2-m};1-m\right);C\left(-\sqrt{2-m};1-m\right)\)

Đáp án C
Tập xác định D = R
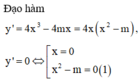
Đồ thị hàm số có 3 điểm cực trị Û y’ = 0 có ba nghiệm phân biệt Û (1) có hai nghiệm phân biệt khác 0 Û m > 0
Với m > 0, các điểm cực trị đó là
![]()
khi đó tam giác ABC là tam giác cân đỉnh A
Để tam giác ABC là tam giác vuông cân