Cho hai góc kề bù AOM và BOM trong đó A O M ^ = 120 0 . Trên nửa mặt phẳng bờ AB không chứa tia OM ta vẽ tia ON sao cho A O N ^ = 60 0 .Hỏi hai góc A O M ^ và B O N ^ có phải là hai góc đối đỉnh không? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có: \(\widehat{AOM}+\widehat{AON}=120^0+60^0\)
\(\Rightarrow\widehat{MON}=180^0\)
=> ON là tia đối của OM
Mà OB là tia đối của OA
=> \(\widehat{AON}\) và \(\widehat{BOM}\)đối đỉnh.

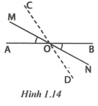
Theo đề bài ta có A O M ^ = M O C ^ , B O N ^ = D O N ^ mà A O M ^ = B O N ^ (hai góc đối đỉnh) nên M O C ^ = D O N ^ .
Ta có M O D ^ + D O N ^ = 180 ° (hai góc kề bù), suy ra M O D ^ + M O C ^ = 180 ° .
Hai góc MOD và MOC là hai góc kề, có tổng bằng 180 ° nên hai tia OC, OD đối nhau.
Chứng tỏ một tia là tia phân giác
Xét hai góc kề bù A O M ^ , A O N ^ Ta có:
A O M ^ + AON ^ = 120 0 + 60 0 = 180 0 .
Vậy hai góc A O M ^ , A O N ^ là hai góc kề bù.
Suy ra hai tia OM, ON đối nhau.
Mặt khác hai tia OA, OB đối nhau
nên hai góc A O M ^ , B O N ^ là hai góc đối đỉnh