Đường tròn có đường kính AC = 2R = 1m. Lực F có phương song song với AC, có chiều không đổi từ A đến C và có độ lớn 600N. Công của lực F sinh ra để làm dịch chuyển vật trên nửa đường tròn AC bằng
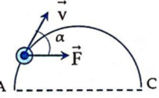
A. 600J
B. 500J
C. 300J
D. 100J
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
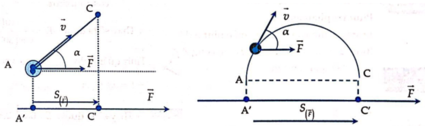
Xét vật di chuyển một cung nhỏ S khi đó cung trùng với dây cung S = AC
Công của lực F di chuyển trên cung này là:
A = F.S.cosα = F. S F ⇀ (*)
Với S F ⇀ = A'C' = AC.cosα chính là độ dài đại số hình chiếu của AC lên phương của lực F ⇀
Xét với một đường cong bất kỳ ta có thể chia nhỏ thành các cung nhỏ tùy ý rồi sử dụng kết quả (*) khi đó ta được công thức cho đường cong tổng quát dài tùy ý
A = F.S.cosα = FS(F→)
Với: F = 600N,S(F→) = A'C' = AC = 1m
Thay vào ta được:
A = F.S.cosα = F.S(F→) = 600.1 = 600J

Đáp án A.


Xét vật di chuyển một cung nhỏ S khi đó cung trùng với dây cung S = AC
Công của lực F di chuyển trên cung này là:
![]()
![]()
chính là độ dài đại số hình chiếu của AC lên phương của lực F →
Xét với một đường cong bất kỳ ta có thể chia nhỏ thành các cung nhỏ tùy ý rồi sử dụng kết quả (*) khi đó ta được công thức cho đường cong tổng quát dài tùy ý



Đáp án C
Do vật di chuyển theo đường cong nên ta áp dụng công thức bổ đề tính công
![]()
với SF chính là độ dài đại số hình chiếu của đường cong lên phương của lực F

=0,3 m


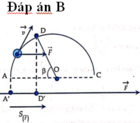
Do vật di chuyển theo đường cong nên ta áp dụng công thức bổ đề tính công
![]()
Với chính là độ dài đại số hình chiếu của đường cong lên phương của lực
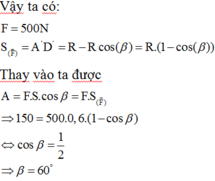


Do vật di chuyển theo đường cong nên ta áp dụng công thức bổ đề tính công
![]()
Với ![]() chính là độ dài đại số hình chiếu của đường cong lên phương của lực F
chính là độ dài đại số hình chiếu của đường cong lên phương của lực F


░░░░░░░░░░░░▄▄
░░░░░░░░░░░█░░█
░░░░░░░░░░░█░░█
░░░░░░░░░░█░░░█
░░░░░░░░░█░░░░█
███████▄▄█░░░░░██████▄
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█████░░░░░░░░░█
██████▀░░░░▀▀█████
k mk đi mk k lại cho

a, Ta có: E C A ^ + O C A ^ = 90 0 và A C H ^ + O A C ^ = 90 0
mà O A C ^ = O C A ^ (do tam giác AOC cân tại O)
Suy ra E C A ^ = A C H ^
Khi đó E A C ^ = H A C ^ (cùng lần lượt phụ với E C A ^ và A C H ^ ), ta có đpcm
b, Chứng minh tương tự suy ra BC là phân giác của F B H ^
Từ đó, chứng minh được BC vuông góc HF (1)
Tam giác ABC có trung tuyến OC = 1 2 AB. Suy ra tam giác ABC vuông tại C , tức là BC vuông góc với AC (2)
Từ (1),(2) suy ra đpcm
c, Ta có : AE+BF =2OC=2R không đổi
d, Ta có A E . B F ≤ A E + B F 2 4 = R 2
suy ra AE.BF lớn nhất = R 2 óAE=BF=R
Điều này xẩy ra khi C là điểm chính giữa cung AB

Ta có : \(A=F.s.cos\alpha=5.6.Cos60^o=15\left(N.m\right)\)
\(\Rightarrow P_{tb}=\dfrac{A}{t}=\dfrac{15}{4}=3,75\left(W\right)\)
Vậy ...
Xét vật di chuyển một cung nhỏ S khi đó cung trùng với dây cung S = AC
Công của lực F di chuyển trên cung này là:
Với chính là độ dài đại số hình chiếu của AC lên phương của lực
chính là độ dài đại số hình chiếu của AC lên phương của lực
Xét với một đường cong bất kỳ ta có thể chia nhỏ thành các cung nhỏ tùy ý rồi sử dụng kết quả (*) khi đó ta được công thức cho đường cong tổng quát dài tùy
Áp dụng công thức bổ đề vừa xây dựng ta có: