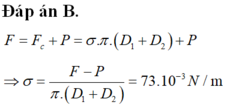Một vòng nhôm có trọng lượng 0,05N, đường kính trong d 1 = 40mm, đường kính ngoài d 2 = 42mm. Cho hệ số căng mặt ngoài của nước là σ = 0,073N/m. Cần phải dùng một lực tối thiểu bằng bao nhiêu để nâng vòng nhôm trên khi nó đặt nằm ngang trong nước (sát mặt nước) ra khỏi mặt nước?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()

Ta có Fc = F – P = σ .2. π . D ⇒ F = P + σ .2. π . D = 0,0906N

Muốn kéo vòng nhôm bứt khỏi mặt thoáng của nước thì cần tác dụng lên nó lực F 1 hướng thẳng đứng lên trên và có cường độ nhỏ nhất bằng tổng trọng lực P của vòng nhôm và lực căng bề mặt F c của nước : F 1 = P + F c
Vì mặt thoáng của nước tiếp xúc với cả mặt trong và mặt ngoài của vòng nhôm nên lực căng bề mặt Fc có độ lớn bằng :
F c = σ π (d + D)
Từ đó suy ra: F 1 = P + σ π (d + D).
Với chất lỏng là nước có σ = 72. 10 - 3 N/m, ta tìm được :
F 1 = 62,8. 10 - 3 + 72. 10 - 3 .3,14.(48 + 50). 10 - 3 ≈ 85. 10 - 3 N

Muốn kéo vòng nhôm bứt khỏi mặt thoáng của nước thì cần tác dụng lên nó lực F 1 hướng thẳng đứng lên trên và có cường độ nhỏ nhất bằng tổng trọng lực P của vòng nhôm và lực căng bề mặt F c của nước : F 1 = P + F c
Vì mặt thoáng của nước tiếp xúc với cả mặt trong và mặt ngoài của vòng nhôm nên lực căng bề mặt Fc có độ lớn bằng :
F c = σ π (d + D)
Từ đó suy ra: F 1 = P + σ π (d + D).
Với chất lỏng là rượu có σ = 22. 10 - 3 N/m, ta tìm được :
F 2 = 62,8. 10 - 3 + 22. 10 - 3 .3,14.(48 + 50). 10 - 3 ≈ 69,5. 10 - 3 N.

Gọi lực căng bề mặt tác dụng lên vòng ngoài và vòng trong lần lượt là: F1, F2
Ta có: Thời điểm vòng gần rời khỏi mặt nước lực đàn hồi của lò xo cân bằng với lực căng bề mặt: Fdh = F
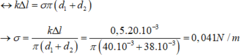
Đáp án: C