Cho tam giác ABC có trực tâm H.
Biểu thức A H → . H B → − H C → + B H → . H C → − H A → + C H → . H A → − H B → bằng
A. 0 →
B.0
C. A B 2 + B C 2 + C A 2
D. 1 2 A B 2 + B C 2 + C A 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì M đối xứng với H qua BC nên BC là đường trung trực của MH
Suy ra: BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM(cmt)
CH=CM(cmt)
BC chung
Do đó: ΔBHC=ΔBMC(c-c-c)

a: Ta có: M và H đối xứng nhau qua BC
nên BC là đường trung trực của MH
Suy ra: BH=BM và CH=CM
Xét ΔBHC và ΔBMC có
BH=BM
HC=MC
BC chung
Do đó: ΔBHC=ΔBMC

Cách làm 2 câu tương tự nhau.
a.
\(\overrightarrow{AB}=\left(2;3\right)\Rightarrow\) đường thẳng AB nhận (3;-2) là 1 vtpt
Phương trình AB (qua A) có dạng:
\(3\left(x-1\right)-2\left(y-1\right)=0\Leftrightarrow3x-2y-1=0\)
\(\overrightarrow{HA}=\left(1;1\right);\overrightarrow{HB}=\left(3;4\right)\)
Do BC vuông góc AH nên nhận (1;1) là 1 vtpt
Phương trình BC (đi qua B) có dạng:
\(1\left(x-3\right)+1\left(y-4\right)=0\Leftrightarrow x+y-7=0\)
Do AC vuông góc HB nên nhận (3;4) là 1 vtpt
Phương trình AC (đi qua A) có dạng:
\(3\left(x-1\right)+4\left(y-1\right)=0\Leftrightarrow3x+4y-7=0\)
Câu b hoàn toàn tương tự

Ta có:
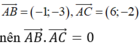
Suy ra tam giác ABC vuông tại A do đó trực tâm H trùng với A
Vậy H( -1 ; 3)
Chọn B.

Chọn D.
Gọi H (x; y) là trực tâm tam giác ABC nên
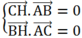
Mà
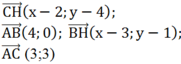
Suy ra:
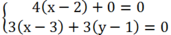
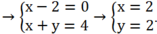
Vậy H(2; 2).

a : Gọi O là giao của HK và CB, ta có:
S của tam giác CHB= \(\frac{1}{2}OH\cdot CB\)
S của tam giác BKC=\(\frac{1}{2}KO\cdot CB\)
Mà ta có K là điểm đối xứng với H qua BC => KO=HO
Nên ta có thể thay
S của tam giác BKC=\(\frac{1}{2}OH\cdot CB\)
Hay \(Sbkc=Sbhc\)
Nếu đúng thì cho mk xin **** nha
Vì H là trực tâm tam giác ABC nên:
A H ⊥ C B ; B H ⊥ A C ; C H ⊥ B A ⇒ A H → . C B → = 0 ; B H → . A C → = 0 ; C H → . B A → = 0
Ta có
A H → . H B → − H C → + B H → . H C → − H A → + C H → . H A → − H B →
= A H → . C B → + B H → . A C → + C H → . B A → = 0
CHỌN B