tìm x,y trong cấc hình sau , giúp với mình đang vội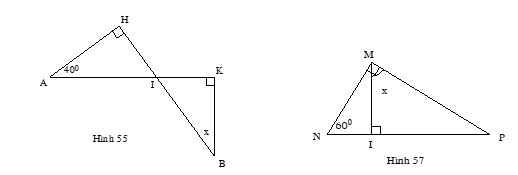
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
$x+10\vdots x+5$
$\Rightarrow (x+5)+5\vdots x+5$
$\Rightarrow 5\vdots x+5$
Mà $x+5\geq 5$ do $x$ là số tự nhiên nên $x+5=5$
$\Rightarrow x=0$

( x - 1 )2018 + (y - 2 )2020+(z-3)2022=0
\(\Leftrightarrow\left\{{}\begin{matrix}x-1=0\\y-2=0\\z-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\\z=3\end{matrix}\right.\)
\(A=\dfrac{1}{9}\left(-x\right)^{2021}y^2z^3=\dfrac{1}{3}\left(-1\right)^{2021}.2^2.3^3=\dfrac{1}{3}.\left(-1\right).4.27=-36\)


Ta có: \(20x+10y=2010\)
\(\Leftrightarrow2x+y=201\)( chia cả 2 vế cho 10)
\(\Leftrightarrow x=\frac{201-y}{2}\)
Do đó, để x nguyên thì 201-y=2k \(\left(k\in Z\right)\)
\(\Leftrightarrow y=201-2k\)
\(\Rightarrow x=\frac{201-201+2k}{2}=k\)
Vậy các cặp số nguyên x,y thỏa mãn phương trình có dạng \(\left(x;y\right)=\left(k;201-k\right)\)với \(k\in Z\)

Hình 55:
Xét tam giác AHI và tam giác BKI lần lượt vg tại H,K có:
\(\left\{{}\begin{matrix}\widehat{HAI}+\widehat{HIA}=90^0\\x+\widehat{KIB}=90^0\end{matrix}\right.\)
Mà \(\widehat{HIA}=\widehat{KIB}\)(đối đỉnh)
\(\Rightarrow x=\widehat{HAI}=40^0\)
Hình 57:
Xét tam giác MNP vg tại M và tam giác MIP vg tại I:
\(\left\{{}\begin{matrix}\widehat{N}+\widehat{NMI}=90^0\\x+\widehat{NMI}=90^0\end{matrix}\right.\)
\(\Rightarrow x=\widehat{N}=60^0\)
x1=40 độ
x2=60 độ
Có cần giải thích chi tiết ko bạn