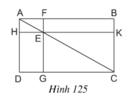
Cho hình chữ nhật ABCD. Qua E là một điểm bất kỳ nằm trên đường chéo AC, kẻ hai đường chéo FG//AD và HK//AB ( F ∈ AB, G ∈ DC, H ∈ AD, K ∈ DC ). Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 1 2018
Ta có: SEHDG = SADC – SAHE – SEGC.
SEFBK = SABC – SAFE – SEKC.
Để chứng minh SEHDG = SEFBK,
ta đi chứng minh SADC = SABC; SAHE = SAFE ; SEGC = SEKC.
+ Chứng minh SADC = SABC.
SADC = AD.DC/2;
SABC = AB.BC/2.
ABCD là hình chữ nhật ⇒ AB = CD, AD = BC
⇒ SADC = SABC.
+ Chứng minh SAHE = SAFE (1)
Ta có: EH // AF và EF // AH
⇒ AHEF là hình bình hành
Mà Â = 90º
⇒ AHEF là hình chữ nhật
⇒ SAHE = SAFE (2)
+ Chứng minh SEGC = SEKC
EK // GC, EG // KC
⇒ EGCK là hình bình hành
Mà D̂ = 90º
⇒ EGCK là hình chữ nhật
⇒ SEGC = SEKC (3).
Từ (1); (2); (3) suy ra đpcm.
15 tháng 12 2017
AF // HE ( HK // AB )
AH // EF ( FC // AD )
\(\Rightarrow\)AHEF là hình bình hành
có : góc HAF = 90 độ ( ABCD là hình chữ nhật )
\(\Rightarrow\)AHEF là hình chữ nhật
EF // CG ( HK // AB // CD )
EG // CK ( FG // AD // BC )
\(\Rightarrow\)EGCK là hình bình hành
có góc GCK = 90 độ ( ABCD là hình chữ nhật )
\(\Rightarrow\)EGCK là hình chữ nhật
Ta có : diện tích ABC = 1/2 AB . BC = 1/2diện tích ABCD
diện tích ACD = 1/2 AD . DC = 1/2 diện tích ABCD
\(\Rightarrow\)Diện tích ABC = diện tích ACD
Tương tự : diện tích AEF = diện tích EHA
diện tích ECK = diện tích CFG
diện tích EFBK = diện tích ABC - diện tích AEF - diện tích ECK
diện tích EGDH = diện tích ACD - diện tích EHA - diện CEG
\(\Rightarrow\) diện tích EFBK = diện tích EGDH ( đpcm )
21 tháng 4 2017
Xem hình 125 ta thấy:
SABC = SADC
SAFE = SAHE
SEKC = SEGC
Suy ra: SABC – SAFE – SEKC = SADC – SAHE - SEGC
hay SEFBK = SEGDH
20 tháng 11 2015
ta có:
SABC = SADC
SAFE = SAHE
SEKC = SEGC
=> SABC – SAFE – SEKC = SADC – SAHE - SEGC
hay SEFBK = SEGDH
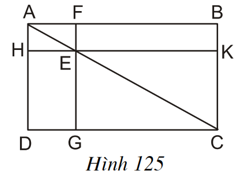
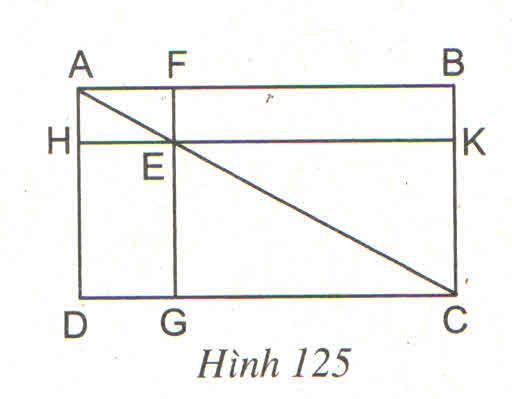
Theo giả thiết ta có FG//AD, HK//AB nên HE//AF và AH//EF.
Xét tứ giác AFEH có: