Tìm hàm số f(x) biết f ' x = 4 x 2 + 4 x + 3 2 x + 1 và f(0)=1 Biết f(x) có dạng: f x = a x 2 + b x + ln 2 x + 1 + c Tìm tỉ lệ của a : b : c
A. a : b : c = 1 : 2 : 1
B. a : b : c = 1 : 1 : 1
C. a : b : c = 2 : 2 : 1
D. a : b : c = 1 : 2 : 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
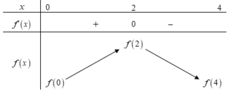
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)

Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)

a ) Ta có : f(2) = 5
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(2\right)\\\text{ax}-3=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\a.2-3=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=2\\a=4\end{cases}}\)
Vậy a = 4
b ) Ta có : f(0) = 3
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(0\right)\\\text{ax}+b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\a.0+b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\b=3\end{cases}}\) ( 1 )
Ta có : f ( 1 ) = 4
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=f\left(1\right)\\\text{ax}+b=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\a.1+b=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\a+b=4\end{cases}}\) ( 2 )
Thay b = 3 ở ( 1 ) vào a+b=4 ở ( 2 ) ta được : a + 3 = 4
a = 1
Vậy a = 1 ; b = 3

a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{2}a\cdot\left(-4\right)+b=-3\\\dfrac{1}{2}a\cdot0+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2a+b=-3\\b=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-3\\a=0\end{matrix}\right.\)
Vậy: f(x)=-3
b: f(1)=f(2)=f(-2)=f(-1)=-3
c: Đặt y=4
=>f(x)=4
=>-3=4(vô lý)

Chọn C.
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.

Bài này chỉ có thể trắc nghiệm (dựa vào kết quả trắc nghiệm để suy luận) chứ không thể giải tự luận
Vì với mỗi hàm \(f\left(x\right)\) khác nhau sẽ cho những khoảng đồng biến - nghịch biến của \(g\left(x\right)\) khác nhau
Đáp án đúng : B