Bằng cách biến đổi các hàm số lượng giác, hãy tính: ∫ sin 4 x . cos 4 x d x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GV
Giáo viên Toán
Giáo viên
4 tháng 5 2017
a) \(\sin^4x=\left(\sin^2x\right)^2=\left(\dfrac{1-\cos2x}{2}\right)^2\)
\(=\dfrac{1}{4}\left(1-2\cos2x+\cos^22x\right)\)
\(=\dfrac{1}{4}\left(1-2.\cos2x+\dfrac{1+\cos4x}{2}\right)\)
\(=\dfrac{3}{8}-\dfrac{1}{2}\cos2x+\dfrac{1}{8}\cos4x\)
Vậy:
\(\int\sin^4x\text{dx}=\int\left(\dfrac{3}{8}-\dfrac{1}{2}\cos2x+\dfrac{1}{8}\cos4x\right)\text{dx}\)
\(=\dfrac{3}{8}x-\dfrac{1}{4}\sin2x+\dfrac{1}{32}\sin4x+C\)
23 tháng 1 2016
Biến đổi :
\(4\sin x+3\cos x=A\left(\sin x+2\cos x\right)+B\left(\cos x-2\sin x\right)=\left(A-2B\right)\sin x+\left(2A+B\right)\cos x\)
Đồng nhất hệ số hai tử số, ta có :
\(\begin{cases}A-2B=4\\2A+B=3\end{cases}\)\(\Leftrightarrow\begin{cases}A=2\\B=-1\end{cases}\)
Khi đó \(f\left(x\right)=\frac{2\left(\left(\sin x+2\cos x\right)\right)-\left(\left(\sin x-2\cos x\right)\right)}{\left(\sin x+2\cos x\right)}=2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\)
Do đó,
\(F\left(x\right)=\int f\left(x\right)dx=\int\left(2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\right)dx=2\int dx-\int\frac{\left(\cos x-2\sin x\right)dx}{\sin x+2\cos x}=2x-\ln\left|\sin x+2\cos x\right|+C\)
PT
1
CM
29 tháng 9 2019
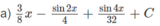
Hướng dẫn:
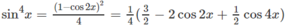
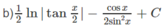
Hướng dẫn: Đặt u = cosx
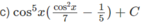
Hướng dẫn: Đặt u = cosx
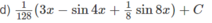
Hướng dẫn:
PT
1
PT
1
PT
1
CM
17 tháng 1 2019
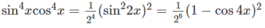
Vì 75 ° + 15 ° = 90 ° nên sin 75 ° = cos 15 °
Vì 53 ° + 37 ° = 90 ° nên cos 53 ° = sin 37 °
Vì 47 ° 20 ' + 42 ° 40 ' = 90 ° nên sin 47 ° 20 ' = cos 42 ° 40 '
Vì 62 ° + 28 ° = 90 ° nên tg 62 ° = cotg 28 °
Vì 82 ° 45 ' + 7 ° 15 ' = 90 ° nên cotg 82 ° 45 ' = tg 7 ° 15 '
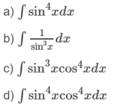
Hướng dẫn: