Tập nghiệm của hệ bất phương trình 3 x + 1 > 4 - x 3 - x > 9 - 6 x là:
A. S = 6 5 ; + ∞
B. S = 3 4 ; 6 5
C. S = 3 4 ; + ∞
D. S = [ 6 5 ; + ∞ )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Ta có: 3 x + 1 > 4 - x 3 - x > 9 - 6 x ⇔ 4 x > 3 5 x > 6 ⇔ x > 3 4 x > 6 5 ⇔ x > 6 5
Do đó, tập nghiệm của hệ bất phương trình là S = 6 5 ; + ∞

Chọn D.
Ta có
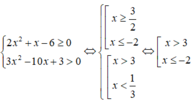
Vậy tập nghiệm hệ bất phương trình là S = ( - ∞ ;-2] ∪ (3; + ∞ ).

\(\dfrac{x^2+x+3}{x^2-4}\ge1\Leftrightarrow\dfrac{x^2+x+3}{x^2-4}-1\ge0\)
\(\Leftrightarrow\dfrac{x+7}{x^2-4}\ge0\Rightarrow\left[{}\begin{matrix}-7\le x< -2\\x>2\end{matrix}\right.\)
\(\Rightarrow S\cap\left(-2;2\right)=\varnothing\)

Đáp án: B
Ta có:
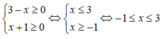
Vậy tập nghiệm của hệ bất phương trình là: [-1;3]

Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
⇒ log m 4 ≤ log m 2 ⇔ log m 2 ≤ 0 ⇔ m ∈ 0 ; 1 .
Khi đó, bất phương trình
log m 2 x 2 + x + 3 ≤ log m 3 x 2 − x ⇔ 3 x 2 − x > 0 2 x 2 + x + 3 ≥ 3 x 2 − x ⇔ − 1 ≤ x < 0 1 3 < x ≤ 3 .

Ta có: |x| < 3 ⇔ -3 < x < 3
Các giá trị trong tập hợp A là nghiệm của bất phương trình là:
-2; -1; 0; 1; 2

Chọn B.
Ta có:
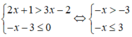
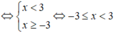
Tập nghiệm của hệ bất phương trình là S = [-3;3).