Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Đường thẳng ( d) có VTCP là u → = ( 3 ; - 4 )
Nên đường thẳng (d) có 1 VTPT là ( 4; 3) .
Do 2 đườg thẳng ∆ và (d) song song với nhau nên chúng có cùng VTPT và cùng VTCP .
Suy ra đường thẳng ∆ có 1 VTPT là (4; 3) .
Đáp án A
Đường thẳng d có một vectơ pháp tuyến là n → = ( - 2 ; - 5 ) nên đường thẳng này có 1 VTCP là: n → = 5 ; - 2
Do đường thẳng d và ∆ song song với nhau nên vecto n → = ( 5 ; - 2 ) cũng là VTCP của đường thẳng ∆.
Đáp án A
Do hai đường thẳng vuông góc với nhau thì VTPT của đường thẳng này là VTCP của đường thẳng kia và ngược lại.
Do đường thẳng ∆ vuông góc với đường thẳng (d) nên nhận VTPT của đường thẳng ( d) là VTCP. Do đó: một VTCP của đường thẳng ∆ là ( 2; -1)
Chọn C.
Đường thẳng Δ vuông góc với d nhận VTPT của d là VTCP
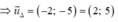
ĐÁP ÁN A
Nếu u → là vectơ chỉ phương của một đường thẳng thì k u → (với k ≠ 0) đều là vectơ chỉ phương của đường thẳng đó.
Vì vậy các vectơ có tọa độ tỉ lệ với u → 2 ; - 3 đều là vectơ chỉ phương.
Ta có: 2 3 ≠ − 3 2 ; 2 − 2 = − 3 3 ; 2 6 = − 3 − 9 ; 2 − 4 = − 3 6
Do đó, trong các vecto đã cho có u 1 → không phải là vecto chỉ phương của đường thẳng ∆.
Đáp án B
Ta có nhận xét:
Hai đường thẳng vuông góc với nhau thì VTPT của đường thẳng này là VTCP của đường thẳng kia và ngược lại.
Do đường thẳng ∆ vuông góc với đường thẳng (d) nên nhận VTCP của đường thẳng (d) là VTPT. Do đó: 1 VTPT của đường thẳng ∆ là ( -2; -3).
Mà hai vectơ (-2; -3) và ( 4; 6) là 2 vectơ cùng phương nên vectơ (4; 6) cũng là VTPT của đường thẳng ∆.