Cho tam giác ABC vuông tại A. Trên tia đối của tia CA, lấy điểm D sao cho cho CA = CD. Trên tia đối của tia CB, lấy điểm E sao cho CB = CE. Số đo góc C D E ^ là:
A. 80 °
B. 90 °
C. 100 °
D. 110 °
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

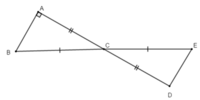


Xét ΔBAC và ΔEDC có
CB=CE
\(\widehat{BCA}=\widehat{ECD}\)
CA=CD
Do đó: ΔBAC=ΔEDC
Suy ra: \(\widehat{CDE}=90^0\)

Xét ΔCAB và ΔCDE có
CA=CD
\(\widehat{ACB}=\widehat{DCE}\)
CB=CE
Do đó: ΔCAB=ΔCDE
Suy ra: \(\widehat{CAB}=\widehat{CDE}\)
hay \(\widehat{CDE}=90^0\)

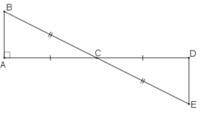
Xét ΔABC và ΔDEC, ta có:
AC = DC (gt)
∠(ACB) =∠(ECD) (đối đỉnh)
BC=EC (gt)
Suy ra: ΔABC= ΔDEC (c.g.c)
⇒∠A =∠D ̂(hai góc tương ứng).Mà ∠A =90o nên ∠D =90o

Xét tứ giác ABDE có
C là trung điểm của AD
C là trung điểm của BE
Do đó: ABDE là hình bình hành
Suy ra: AB//DE
hay DE⊥AC
=>\(\widehat{CDE}=90^0\)

a) Áp dụng định lí tổng 3 góc trong 1 tam giác ta có :
\(\widehat{A}+\widehat{B}+\widehat{C}=180^O\)
hay \(90^o+50^o+\widehat{C}=180^o\)
\(\Rightarrow\widehat{C}=180^o-90^o-50^o=40^o\)
b) Xét \(\Delta ABCvà\Delta DECcó\)
AC = DC ( gt )
CB = CE ( gt )
\(\widehat{ECD}=\widehat{BCA}\) ( đối đỉnh )
\(\Rightarrow\Delta ABC=\Delta DEC\) ( c.g.c )
c) \(\Rightarrow\widehat{E}=\widehat{B}\) ( 2 góc tương ứng )
mà 2 góc này ở vị trí so le trong
\(\Rightarrow AB//DE\)
câu d mik chịu nhe !!!

Hình bạn tự vẽ nhé!
Xét tam giác ABC và tam giác DEC có:
CB = CE (gt)
góc BCA = góc ECD ( đối đỉnh)
CA = CD (gt)
=> Tam giác ABC = Tam giác DEC (c.g.c)
=> góc CAB = góc CDE (2 góc tương ứng)
mà góc CAB = 90 độ
=> góc CDE = 90 độ.
Vậy góc CDE = 90 độ

xét tg abc và tg edc có
bc = ec ( gt )
góc bca = góc dce ( 2 góc đối đỉnh )
ac = dc
abc = edc
suy ra góc bac = góc cde = 90 độ