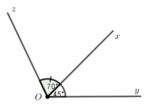
Cho góc x O y ^ = 45 ∘ . Trên nửa mặt phẳng bờ Ox không chứa tia Oy vẽ x O z ^ = 70 ∘ . Trong ba tia Ox, Oy, Oz tia nào nằm giữa hai tia còn lại? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 6 2017
Trên nửa mặt phẳng bờ Ox có x O y ^ < x O t ^ nên tia Oy nằm giữa hai tia Ox, Ot
CM
25 tháng 6 2017
Vì tia Ox nằm giữa hai tia Ozvà Oy nên
x O z ^ + x O y ^ = z O y ^ 70 ∘ + 45 ∘ = z O y ^ z O y ^ = 115 ∘
CM
10 tháng 9 2017
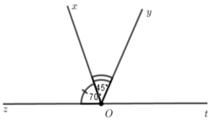
Vì z O x ^ và z O x ^ là hai góc kề bù nên
z O x ^ + x O t ^ = 180 ∘ 70 ∘ + x O t ^ = 180 ∘ x O t ^ = 180 ∘ − 70 ∘ x O t ^ = 110 ∘
20 tháng 2 2021
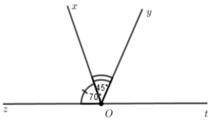
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox có hai tia Oz và Oy mà ˆ x O z < ˆ x O y ( 350 < 700 ) => Oz nằm giữa Ox và Oy
b) => ˆ x O z + ˆ z O y = ˆ x O y 350 + ˆ z O y = 700 ˆ z O y = 700 - 350 = 350 => ˆ x O z = ˆ z O y = 350
c) Vì Oz nằm giữa Ox, Oy và ˆ x O z = ˆ z O y = 350 => Oz là tia phân giác của ˆ x O y
10 tháng 6 2016
a) (Sửa lại là xOy và x'Oy' đối đỉnh nha, k có t trog đề bài 
)
Ta có : \(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-45^o=135^o\)
Oy là tia phân giác của góc x'Oy' nên \(\widehat{x'Oy'}=\frac{1}{2}\widehat{x'Oz}=\frac{1}{2}.90^o=45^o\)
Do đó \(\widehat{x'Oy}+\widehat{x'Oy'}=135^o+45^o=180^o\) => Oy, Oy' là 2 tia đối nhau (1)
; đã có điểm O trên đg thẳng xx' nên Ox, Ox' đối nhau (2)
Từ (1) và (2) => góc xOy và x'Oy' đối đỉnh
b) Ta có : \(\widehat{xOy}+\widehat{yOt}+\widehat{x'Ot}=180^o\) (kề bù)
=> \(\widehat{x'Ot}=180^o-45^o-90^o=45^o\)
Vì tia Oz thuộc nửa mặt phẳng bờ Ox không chứa tia Oy nên tia Ox nằm giữa hai tia Oz và Oy