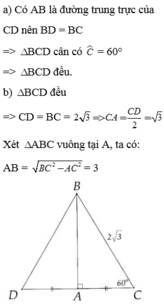
Cho tam giác ABC vuông tại A có góc C ^ = 60 ° . Lấy điểm D đối xứng với điểm C qua AB.
a) Chứng minh tam giác BCD là tam giác đều.
b) Biết B C = 2 3 . Tính độ dài các cạnh AB, AC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
28 tháng 9 2017
Đúng(0)
Những câu hỏi liên quan
5 tháng 2 2023
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hình chữ nhật
b: Gọi giao của AH và BC là N
=>N là trung điểm của AH
=>BN là phân giác của góc ABH
=>góc ABN=góc HBN
=>góc HBC=góc ABN=góc DCB
c: Xet ΔAHD có
N,M lần lượt là trung điểm của AH,AD
nên NM là đường trung bình
=>NM//DH và NM=DH/2
=>DH//BC
mà góc DCB=góc HBC
nên DHBC là hình thang cân
30 tháng 3 2021
a) Xét ΔABH vuông tại H và ΔADH vuông tại H có
AH chung
BH=DH(gt)
Do đó: ΔABH=ΔADH(hai cạnh góc vuông)
Suy ra: AB=AD(hai cạnh tương ứng)
Xét ΔABD có AB=AD(cmt)
nên ΔABD cân tại A(Định nghĩa tam giác cân)
Xét ΔABD cân tại A có \(\widehat{ABD}=60^0\)(gt)
nên ΔABD đều(Dấu hiệu nhận biết tam giác đều)
30 tháng 6 2023
a: Xet ΔABC vuông tại B và ΔAHB vuông tại H có
góc A chung
=>ΔABC đồng dạng với ΔAHB
b: Xét ΔDEC vuông tại D và ΔHEB vuông tại H có
góc DEC=góc HEB
=>ΔDEC đồng dạng với ΔHEB
=>DE/HE=DC/HB=EC/EB
=>DC*EB=HB*EC
c: ED/EH=EC/EB
=>ED/EC=EH/EB
=>ΔEDH đồng dạng với ΔECB
e:
Xét ΔCFB có
BD,CH là đường cao
BD cắt CH tại E
=>E là trực tâm
=>FE vuông góc BC
=>FE//AB
Xét ΔHBA vuông tại H và ΔHFE vuông tại H có
HA=HE
góc HBA=góc HFE
=>ΔHBA=ΔHFE
=>HB=HF
Xét tứ giác BEFA có
BF cắt EA tại trung điểm của mỗi đường
BF vuông góc EA
=>BEFA là hình thoi
