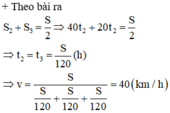Một ô tô chuyển động trên đoạn đường AB. Nửa quãng đường đầu ô tô đi với vận tốc 60 km/h, nửa quãng đường còn lại ô tô đi với nửa thời gian đầu với vận tốc 40 km/h, nửa thời gian sau đi với vận tốc 20 km/h. Xác định vận tốc trung bình cả cả quãng đường AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VT
Vũ Thành Nam
29 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
VT
10 tháng 7 2019
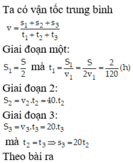
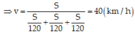
Giải:
Ta có vận tốc trung bình v = s 1 + s 2 + s 3 t 1 + t 2 + t 3
Giai đoạn một: S 1 = S 2 mà t 1 = S 1 v 1 = S 2 v 1 = 2 120 ( h )
Giai đoạn 2: S 2 = v 2 . t 2 = 40. t 2
Giai đoạn 3: S 3 = v 3 . t 3 = 20. t 3 mà t 2 = t 3 ⇒ s 3 = 20 t 2
Theo bài ra S 2 + S 3 = S 2 ⇒ 40 t 2 + 20 t 2 = S 2 ⇒ t 2 = t 3 = S 120 ( h )
⇒ v = S S 120 + S 120 + S 120 = 40 k m / h
19 tháng 7 2016
Gọi độ dài đoạn Ab là x(km).Gọi các đoạn(đi với vận tõc khác nhau) lần lượt là I,II,III.
Thời gian đi được trong đoạn I:
t1=s1/v1=(1/2x)/60=x/120h
Thời gian đi đoạn II:
t2=s2/v2=(1/4x)/40=x/160h
Thời gian đi đoạn III:
t3=s3/v3=(1/4x)/20=x/80h
Vận tốc trung bình trên cả đoạn đường AB(km/h)
V=(s1+s2+s3)/(t1+t2+t3)
=x/(x/120+x/160+x/80)
=x/[x/40.(1/3+1/4+1/2)]
=x/(13x/480)=480/13
=37km/h
12 tháng 8 2016
gọi thời gian, vận tốc, nửa đoạn đường đầu lần lượt là t1, v1 , S1
gọi nửa đoạn đường sau là S2
gọi nửa thời gian đầuvà sau của nửa đoạn đường còn lại là t2 và t3
gọi vận tốc của nửa đoạn đường sau trong hai giai đoạn là v2 và v3
ta có :
vtb = \(\frac{S1+S2}{t1+t2+t3}\) =\(\frac{S}{t1+t2+t3}\) =\(\frac{S}{\frac{S1}{v1}+\frac{S2}{v2+v3}}\) =\(\frac{S}{\frac{S}{\frac{2}{v1}}+\frac{S}{\frac{2}{v2+v3}}}\) =\(\frac{S}{\frac{S}{2v1}+\frac{S}{2.\left(v2+v3\right)}}\) = \(\frac{S}{S.\left(\frac{1}{2.60}+\frac{1}{2.\left(40+20\right)}\right)}\) =\(\frac{1}{\frac{1}{120}+\frac{1}{120}}\) =\(\frac{1}{\frac{2}{120}}\) = 60 km/h
14 tháng 1 2022
a) Ta có: \(\left\{{}\begin{matrix}t_1=\dfrac{S_1}{v_1}=\dfrac{S}{2v_1}=\dfrac{S}{40}\left(h\right)\\t_2=\dfrac{S_2}{v_2}=\dfrac{S}{2v_2}=\dfrac{S}{120}\left(h\right)\end{matrix}\right.\)
Vận tốc TB ô tô đi từ M đến N:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{120}}=\dfrac{S}{S\left(\dfrac{1}{40}+\dfrac{1}{120}\right)}=30\left(\dfrac{km}{h}\right)\)
b) Ta có: \(\left\{{}\begin{matrix}S_1'=t_1'.v_1=20t\left(km\right)\\S_2'=t_2'.v_2=60t\left(km\right)\end{matrix}\right.\)
Vận tốc TB ô tô đi từ N về M:
\(v_{tb}'=\dfrac{S_1'+S_2'}{t_1'+t_2'}=\dfrac{20t+60t}{2t}=40\left(\dfrac{km}{h}\right)\)
Thời gian đi và thời gian về lần lượt là:
\(t=\dfrac{S}{30}\left(h\right),t'=\dfrac{S}{40}\left(h\right)\Rightarrow t>t'\)
Vậy thời gian đi nhiều hơn thời gian về
d) Theo đề bài ta có:
\(t-t'=0,5\Rightarrow\dfrac{S}{30}-\dfrac{S}{40}=0,5\Rightarrow S\left(\dfrac{1}{30}-\dfrac{1}{40}\right)=0,5\Rightarrow S_{MN}=60\left(km\right)\)
